题目内容
9.如图是抛物线形拱桥,当水面在L时,拱顶离水面2米,水面宽4米,水位下降1米后,求水面的宽是多少米?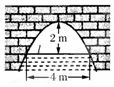
分析 先建立直角坐标系,将A点代入抛物线方程求得m,得到抛物线方程,再把y=-3代入抛物线方程求得x0进而得到答案.
解答  解:如图建立直角坐标系,设抛物线方程为x2=my,
解:如图建立直角坐标系,设抛物线方程为x2=my,
将A(2,-2)代入x2=my,
得m=-2
∴x2=-2y,代入B(x0,-3)得x0=$\sqrt{6}$,
故水面宽为2$\sqrt{6}$m.
点评 本题主要考查抛物线的应用.考查了学生利用抛物线解决实际问题的能力.

练习册系列答案
相关题目
19.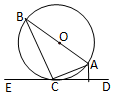 如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )
 如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
19.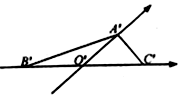 已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图,其中 B'O'=C'O'=1,${A}'{O}'=\frac{{\sqrt{3}}}{2}$,那么对于原△ABC则有( )
已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图,其中 B'O'=C'O'=1,${A}'{O}'=\frac{{\sqrt{3}}}{2}$,那么对于原△ABC则有( )
 已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图,其中 B'O'=C'O'=1,${A}'{O}'=\frac{{\sqrt{3}}}{2}$,那么对于原△ABC则有( )
已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图,其中 B'O'=C'O'=1,${A}'{O}'=\frac{{\sqrt{3}}}{2}$,那么对于原△ABC则有( )| A. | AB=BC | B. | AB=BC,且AB⊥BC | C. | AB⊥BC | D. | AB=AC,且AB⊥AC |
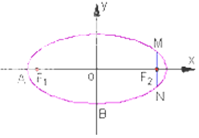 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),b=1,左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M,N两点,且|MN|=1.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),b=1,左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M,N两点,且|MN|=1.