题目内容
14.已知正三棱锥S-ABC,底面是边长为1的正三角形,侧棱长为2,若过直线AB的截面,将正三棱锥的体积分成两个相等的部分,则截面与底面所成二面角的平面角的余弦值为( )| A. | $\frac{\sqrt{15}}{10}$ | B. | $\frac{4\sqrt{15}}{15}$ | C. | $\frac{\sqrt{15}}{15}$ | D. | $\frac{2\sqrt{15}}{15}$ |
分析 根据三棱锥的体积关系确定E是SC的中点,结合二面角平面角的定义进行求解即可.
解答 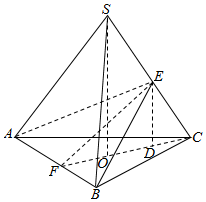 解:设截面为ABE,
解:设截面为ABE,
过S作SO⊥平面ABC,过E作ED⊥平面ABC,
∵过直线AB的截面,将正三棱锥的体积分成两个相等的部分,
∴VE-ABC=$\frac{1}{2}$VS-ABC,
即ED=$\frac{1}{2}$SO,
则E是SC的中点,
取AB的中点F,连接EF,CF,则∠EFC是截面与底面所成二面角的平面角,
∵底面是边长为1的正三角形,侧棱长为2,
∴CF=$\frac{\sqrt{3}}{2}$,CO=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$,OD=CD=$\frac{1}{2}CO=\frac{1}{2}×$$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{6}$,
则SO=$\sqrt{S{C}^{2}-O{C}^{2}}$=$\sqrt{4-(\frac{\sqrt{3}}{3})^{2}}$=$\frac{\sqrt{33}}{3}$,DE=$\frac{1}{2}$SO=$\frac{\sqrt{33}}{6}$,
则EF=$\sqrt{E{D}^{2}+D{F}^{2}}$=$\sqrt{(\frac{\sqrt{33}}{6})^{2}+(\frac{\sqrt{3}}{3})^{2}}$=$\sqrt{\frac{5}{4}}$=$\frac{\sqrt{5}}{2}$,
则cos∠EFC=$\frac{DF}{EF}$=$\frac{\frac{\sqrt{3}}{3}}{\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{15}}{15}$,
故选:D.
点评 本题主要考查二面角的计算和求解,根据三棱锥的体积关系确定E是中点.根据二面角的定义作出平面角是解决本题的关键.

 应用题作业本系列答案
应用题作业本系列答案| A. | {x|-1≤x$<\frac{1}{3}$} | B. | {x|-$\frac{1}{3}<x<2$} | C. | {x|-1$≤x≤\frac{1}{3}$} | D. | {x|-$\frac{1}{3}≤x≤2$} |
 如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB,CE=$\sqrt{2}$CD.
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB,CE=$\sqrt{2}$CD.