题目内容
已知直线l过点(1,4).
(1)若直线l与直线y=2x平行,求直线l的方程;
(2)若直线l与直线y=
x+1垂直,求直线l的方程.
(1)若直线l与直线y=2x平行,求直线l的方程;
(2)若直线l与直线y=
| 1 |
| 3 |
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(1)由已知求得所求直线的斜率,代入直线方程的点斜式,化为一般式得答案;
(2)由已知求得所求直线的斜率,代入直线方程的点斜式,化为一般式得答案.
(2)由已知求得所求直线的斜率,代入直线方程的点斜式,化为一般式得答案.
解答:
解:(1)∵所求直线与直线y=2x平行,
∴所求直线的斜率为2,由直线过点(1,4),
则直线方程为y-4=2(x-1),整理得:2x-y+2=0;
(2)∵所求直线与直线y=
x+1垂直,
∴所求直线的斜率为-3,由直线过点(1,4),
则直线方程为y-4=-3(x-1),整理得:3x+y-7=0.
∴所求直线的斜率为2,由直线过点(1,4),
则直线方程为y-4=2(x-1),整理得:2x-y+2=0;
(2)∵所求直线与直线y=
| 1 |
| 3 |
∴所求直线的斜率为-3,由直线过点(1,4),
则直线方程为y-4=-3(x-1),整理得:3x+y-7=0.
点评:本题考查了直线的一般式方程与直线平行和垂直的关系,考查了直线方程的点斜式,是基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
将函数y=3sin(2x-
)的图象向左平移
单位得到函数的图象y=f(x),则函数y=f(x)图象的一条对称轴是( )
| π |
| 6 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
圆x2+y2=2与圆x2+y2+4y+3=0的位置关系是( )
| A、相离 | B、外切 | C、内切 | D、相交 |
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象的第一部分如图所示,则( )
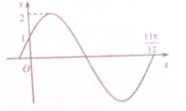
| π |
| 2 |

| A、f(x)的最小正周期为2π | ||
B、f(x)的图象关于直线x=
| ||
C、f(x)的图线关于点(
| ||
D、f(x)在[0,
|
下列命题正确的是( )
| A、直线a与平面α不平行,则a与平面α内的所有直线都不平行 |
| B、直线a与平面α不垂直,则a与平面α内的所有直线都不垂直 |
| C、异面直线a,b不垂直,则过a的任何平面与b都不垂直 |
| D、若直线a和b共面,直线b和c共面,则a和c共面 |
已知函数f(x)=
,下列结论正确的是( )
|
| A、f(x)是奇函数 |
| B、f(x)在(-∞,+∞)上是增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[-1,+∞) |