题目内容
13.化简:$\frac{cos(α+π)•sin^2(α+π)}{tan^2(π+α)•cos^3α}$=-1.分析 直接利用诱导公式及同角三角函数的基本关系式化简求值.
解答 解:$\frac{cos(α+π)•sin^2(α+π)}{tan^2(π+α)•cos^3α}$=$\frac{-cosα•si{n}^{2}α}{ta{n}^{2}α•co{s}^{3}α}$=$-\frac{cosα•si{n}^{2}α}{\frac{si{n}^{2}α}{co{s}^{2}α}•co{s}^{3}α}=-1$.
故答案为:-1.
点评 本题考查三角函数的化简求值,主要考查诱导公式及同角三角函数基本关系式的应用,是基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.若执行如图所示的程序框图,输入x1=1,x2=2,x3=3,$\overline{x}$=2,则输出的数S等于( )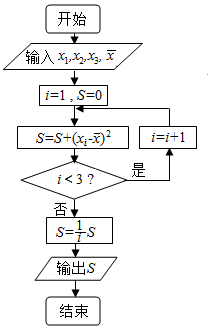

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
1.已知等差数列{an}和{bn} 的前n项和S分别为Sn、Tn,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+1}{n+3}$,则$\frac{{a}_{2}+{a}_{5}+{a}_{17}+{a}_{22}}{{b}_{8}+{b}_{10}+{b}_{12}+{b}_{16}}$=( )
| A. | $\frac{31}{5}$ | B. | $\frac{32}{5}$ | C. | 6 | D. | 7 |
5.已知在平面直角坐标系xOy中,角α的终边在直线y=$\sqrt{2}$x位于第一象限的部分,则sin(α+$\frac{π}{6}$)=( )
| A. | $\frac{3\sqrt{2}-\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}-3\sqrt{2}}{6}$ | C. | $\frac{3\sqrt{2}+\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}+3\sqrt{2}}{6}$ |