题目内容
若关于x的不等式x2+|x+3a|<2至少有一个正数解,则实数a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
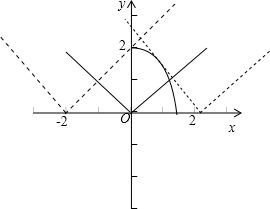
分析:我们将原不等式变形为:|x+3a|<2-x2,我们在同一坐标系画出y=2-x2(y>0,x>0)和 y=|x|两个图象,利用数形结合思想,易得实数a的取值范围.
解答:
 解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.
解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.
在同一坐标系画出y=2-x2(y>0,x>0)和 y=|x|两个函数图象,
将绝对值函数 y=|x|向左移动当右支经过 (0,2)点,-3a=-2,求得a=
.
将绝对值函数 y=|x|向右移动让左支与抛物线y=2-x2(y>0,x>0)相切时,
由
可得x2-x-3a-2=0,由判别式△=0,求得a=-
.
数形结合可得,实数a的取值范围是(-
,
),
故答案为:(-
,
).
 解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.
解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.在同一坐标系画出y=2-x2(y>0,x>0)和 y=|x|两个函数图象,
将绝对值函数 y=|x|向左移动当右支经过 (0,2)点,-3a=-2,求得a=
| 2 |
| 3 |
将绝对值函数 y=|x|向右移动让左支与抛物线y=2-x2(y>0,x>0)相切时,
由
|
| 3 |
| 4 |
数形结合可得,实数a的取值范围是(-
| 3 |
| 4 |
| 2 |
| 3 |
故答案为:(-
| 3 |
| 4 |
| 2 |
| 3 |
点评:本题考查的知识点是一元二次函数的图象,及绝对值函数图象,其中在同一坐标中,画出y=2-x2(y>0,x>0)和 y=|x|两个图象,结合数形结合的思想得到答案,是解答本题的关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
总体容量为203,若采用系统抽样法进行抽样,当抽样间距为多少时不需要剔除个体( )
| A、4 | B、5 | C、6 | D、7 |
在平面直角坐标系中,不等式|y-2|+|x+2|≤2表示的平面区域的面积是( )
| A、8 | ||
| B、4 | ||
C、4
| ||
D、2
|
cos17°sin43°+sin163°sin47°( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|

 已知三次函数f(x)=ax3+bx2+cx+d(a≠0)的图象必有一个对称中心.判断其图象的对称中心的流程图如图所示.对于函数f(x)=
已知三次函数f(x)=ax3+bx2+cx+d(a≠0)的图象必有一个对称中心.判断其图象的对称中心的流程图如图所示.对于函数f(x)=