题目内容
从8名男学生、4名女学生中选出3人参加朗诵比赛,
(1)恰有2名女生的选法有多少种?
(2)至少有1名女生的选法有多少种?
(1)恰有2名女生的选法有多少种?
(2)至少有1名女生的选法有多少种?
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)先从4名女学生中选出2名女生,再从8名男生中选出1人,根据分步计数原理得,问题得以解决
(2)利用间接法,从8名男学生、4名女学生中任选出3人,再排除全是男生的,问题得以解决
(2)利用间接法,从8名男学生、4名女学生中任选出3人,再排除全是男生的,问题得以解决
解答:
解:(1)先从4名女学生中选出2名女生,再从8名男生中选出1人,根据分步计数原理得,故恰有2名女生的选法有
•
=48种,
(2)利用间接法,从8名男学生、4名女学生中任选出3人,再排除全是男生的,故至少有1名女生的选法有
-
=164
| C | 2 4 |
| C | 1 8 |
(2)利用间接法,从8名男学生、4名女学生中任选出3人,再排除全是男生的,故至少有1名女生的选法有
| C | 3 12 |
| C | 3 8 |
点评:本题考查组合数公式的运用,解本题采用排除法较为简单,出现最多、至少一类问题时,常见的方法是间接法.

练习册系列答案
相关题目
已知函数f(x)=sinx+cosx,x∈R,则下列结论正确的是( )
| A、f(x)是奇函数 | ||
| B、f(x)的值域为[-2,2] | ||
C、f(x)关于点(-
| ||
D、f(x)有一条对称轴为x=
|
函数f(x)的导函数f′(x)的图象如图所示,则下列说法正确的是( )
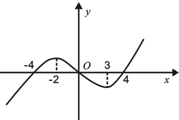

| A、函数f(x)在(-2,3)内单调递减 |
| B、函数f(x)在x=3处取极小值 |
| C、函数f(x)在(-4,0)内单调递增 |
| D、函数f(x)在x=4处取极大值 |
下列结论正确的是( )
A、x>1⇒
| ||||
B、x+
| ||||
C、x>y⇒
| ||||
| D、x>y⇒x2>y2 |