题目内容
已知曲线C1:
(θ为参数)与曲线C2:
(t为参数)有且只有一个公共点,则实数k的取值范围为 .
|
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把曲线C1化为普通方程,把曲线C2代入C1中,由两曲线有且只有一个公共点,△=0;求出k的值.
解答:
解:把曲线C1:
(θ为参数)
化为普通方程是
+y2=1,
把曲线C2
(t为参数)代入C1中,
得
+(kt-2)2=1,
即(2k2+1)-8kt+6=0;
∵两曲线有且只有一个公共点,
∴△=0;
即64k2-24(2k2+1)=0,
解得k=±
.
故答案为:±
.
|
化为普通方程是
| x2 |
| 2 |
把曲线C2
|
得
| t2 |
| 2 |
即(2k2+1)-8kt+6=0;
∵两曲线有且只有一个公共点,
∴△=0;
即64k2-24(2k2+1)=0,
解得k=±
| ||
| 2 |
故答案为:±
| ||
| 2 |
点评:本题考查了参数方程的应用问题,解题时应把参数方程化为普通方程,再结合题意进行解答问题,是基础题.

练习册系列答案
相关题目
已知A(1,-2),若向量
与
=(2,-3)反向,|
|=4
,则点B的坐标为( )
| AB |
| a |
| AB |
| 13 |
| A、(10,7) |
| B、(-10,7) |
| C、(7,-10) |
| D、(-7,10) |
六个同学平均分到甲乙两个班中,分配的种数是( )
| A、20 | B、40 | C、60 | D、80 |
互相平行的三条直线,最多可以确定的平面个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
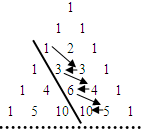 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为 已知蟑螂活动在如图所示的平行四边形OABC内,现有一种利用声波消灭蟑螂的机器,工作时,所发出的圆弧型声波DFE从坐标原点O向外传播,若D是DFE弧与x轴的交点,设OD=x,(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )
已知蟑螂活动在如图所示的平行四边形OABC内,现有一种利用声波消灭蟑螂的机器,工作时,所发出的圆弧型声波DFE从坐标原点O向外传播,若D是DFE弧与x轴的交点,设OD=x,(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )


