题目内容
16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知(2c-a)cosB=bcosA,且b=6.(1)求角B的大小;
(2)设△ABC的两条中线AE、CF相交于点D,求四边形BEDF面积的最大值.
分析 (1)由题意和正弦定理以及三角函数公式可得cosB=$\frac{1}{2}$,可得B=$\frac{π}{3}$;
(2)由余弦定理和基本不等式可得ac≤36,由重心的性质和不等式的性质可得.
解答 解:(1)∵在△ABC中(2c-a)cosB=bcosA,
∴由正弦定理可得(2sinC-sinA)cosB=sinBcosA,
∴2sinCcosB=sinAcosB+sinBcosA=sin(A+B),
∴2sinCcosB=sinC,约去sinC可得cosB=$\frac{1}{2}$,
∴B=$\frac{π}{3}$;
(2)由余弦定理可得36=a2+c2-2accosB=a2+c2-ac≥2ac-ac,
∴ac≤36,当且仅当a=c=6时取等号,如图D为△ABC重心,
∴四边形BEDF面积S=$\frac{1}{3}$S△ABC=$\frac{1}{6}$acsinB=$\frac{\sqrt{3}}{12}$ac≤3$\sqrt{3}$,
∴四边形BEDF面积的最大值为3$\sqrt{3}$,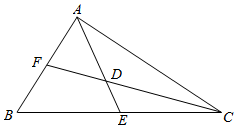
点评 本题考查正余弦定理解三角形,涉及三角函数公式和三角形的面积公式以及重心的性质,属中档题.

练习册系列答案
相关题目
11.已知a,b∈(0,1),则函数f(x)=ax2-4bx+1在区间[1,+∞)上是增函数的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
8.若偶函数f(x)在(-∞,0]上单调递减,a=f(log23),b=f(-1),c=f(2${\;}^{\frac{3}{2}}$),则a,b,c满足( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
6.将函数y=sin2x的图象向左平移φ(φ>0)个单位,得到g(x)的图象,若g(x)的图象关于直线x=$\frac{π}{3}$对称,则φ的最小值为( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |