题目内容
9.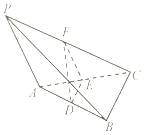 已知,如图,P是平面ABC外一点,PA不垂直于平面ABC,E,F分别是线段AC,PC的中点,D是线段AB上一点,AB=AC,PB=PC,DE⊥EF.
已知,如图,P是平面ABC外一点,PA不垂直于平面ABC,E,F分别是线段AC,PC的中点,D是线段AB上一点,AB=AC,PB=PC,DE⊥EF.(1)求证:PA⊥BC;
(2)求证:BC∥平面DEF.
分析 (1)设线段BC的中点为G,分别连接AG、PG.构建线面垂直:BC⊥平面AGP.根据线面垂直的性质证得结论;
(2)利用三角形中位线定理推知EF∥AP.结合已知条件得到PA⊥DE. 因为PA⊥BC,BC、DE是平面ABC内两条直线,如果BC、DE相交,则PA⊥平面ABC,与PA不与平面ABC的垂直矛盾.
故BC∥DE.最后根据线面平行的判定定理得到结论.
解答 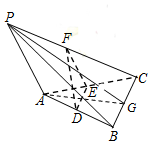 (1)证明:设线段BC的中点为G,分别连接AG、PG.
(1)证明:设线段BC的中点为G,分别连接AG、PG.
∵AB=AC,PB=PC,
∴AG⊥BC,PG⊥BC,
∵AG、PG是平面AGP内的两条相交线,
∴BC⊥平面AGP.
∵PA?平面AGP,
∴PA⊥BC.
(2)证明:∵E、F分别是线段AC、PC的中点,
∴EF∥AP.
∵DE⊥EF,
∴PA⊥DE.
因为PA⊥BC,BC、DE是平面ABC内两条直线,
如果BC、DE相交,则PA⊥平面ABC,与PA不与平面ABC的垂直矛盾.
∴BC∥DE.
又BC?平面DEF,DE?平面DEF,
∴BC∥平面DEF.
点评 本题考查了空间线面面面平行与垂直的判定及性质定理、三角形中位线定理,考查了空间想象能力、推理能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
19.函数y=x$\sqrt{1-{x^2}}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 即是奇函数又是偶函数 | D. | 非奇非偶函数 |
20.等差数列{an}的前10项和为30,前20项和为100,则它的前30项和是( )
| A. | 130 | B. | 170 | C. | 210 | D. | 260 |
1.若$\left\{{1,a,\frac{b}{a}}\right\}=\left\{{0,{a^2},a+b}\right\}$,则a2017+b2017的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
18.幂函数y=x-1不具有的特性是 ( )
| A. | 在定义域内是减函数 | B. | 图象过定点(1,1) | ||
| C. | 是奇函数 | D. | 其定义域是R |
19.已知直线m过点A(2,-3),且在两个坐标轴上的截距相等,则直线m的方程是( )
| A. | 3x+2y=0 | B. | x+y+1=0 | ||
| C. | x+y+1=0或3x+2y=0 | D. | x+y-1=0或3x-2y=0 |