题目内容
2.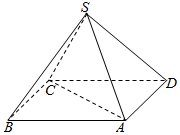 如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等
如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等(1)求证:直线AC垂直于直线SD.
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
分析 (1)连结AC,BD,由正方形的性质得出AC⊥BD,由等腰三角形三线合一得出AC⊥SO,故而AC⊥平面SBD,于是AC⊥SD;
(2)正四棱锥的棱长为3,计算棱锥的高和底面积,代入体积公式计算四棱锥的体积.
解答 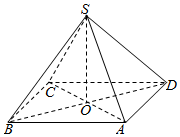 解:(1)连接AC,BD交于点O,则O为线段BD中点,
解:(1)连接AC,BD交于点O,则O为线段BD中点,
∵四边形ABCD是正方形,∴AC⊥BD.
在△SBD中,∵SA=SC,∴SO⊥AC,
∵SO∩BD=O,SO?平面SBD,BD?平面SBD,
∴AC⊥平面SBD,∵SD?平面SBD,
∴AC⊥SD
(2)由题意得正四棱锥边长为3米.
∴BO=$\frac{1}{2}BD$=$\frac{3\sqrt{2}}{2}$.
棱锥的高SO=$\sqrt{S{B}^{2}-O{B}^{2}}$=$\sqrt{9-(\frac{3\sqrt{2}}{2})^{2}}$=$\frac{3\sqrt{2}}{2}$.
∴$V=\frac{1}{3}•{3^2}•\frac{{3\sqrt{2}}}{2}=\frac{{9\sqrt{2}}}{2}$立方米.
答:需要$\frac{{9\sqrt{2}}}{2}$立方米填充材料.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
14.函数f(x)为定义在R上的奇函数,且在(0,+∞)上为增函数,f(3)=0,则不等式f(2x-1)≥0的解为( )
| A. | $[{-1,\frac{1}{2}})∪[{2,+∞})$ | B. | $[{-1,\frac{1}{2}}]∪({2,+∞})$ | C. | [2,+∞) | D. | $[{-1,\frac{1}{2}})$ |
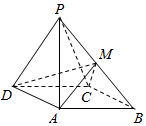 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.