题目内容
10. 某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):(Ⅰ)若教学满意度不低于9.5分,则称该生对教师的教学满意度为“极满意”.求从这16人中随机选取3人,至少有1人是“极满意”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校所有学生中(学生人数很多)任选3人,记X表示抽到“极满意”的人数,求X的分布列及数学期望.
分析 (Ⅰ)设Ai表示所取得人中有i个人是“极满意”,至少有一人是“极满意”记为事件A,利用古典概率计算公式与相互对立事件的概率计算公式即可得出.
(II)X的可能取值为0,1,2,3,由已知得$X-B({3,\frac{1}{4}})$,即可得出.
解答 解:(Ⅰ)设Ai表示所取得人中有i个人是“极满意”,至少有一人是“极满意”记为事件A,
则$P(A)=1-P({A_0})=1-\frac{{C_{12}^3}}{{C_{16}^3}}=\frac{17}{28}$.
(Ⅱ)X的可能取值为0,1,2,3,由已知得$X-B({3,\frac{1}{4}})$.
∴$P({X=0})={({\frac{3}{4}})^3}=\frac{27}{64}$,$P({X=1})=C_3^1({\frac{1}{4}})×{({\frac{3}{4}})^2}=\frac{27}{64}$,$P({X=2})=C_3^2{({\frac{1}{4}})^2}×({\frac{3}{4}})=\frac{9}{64}$,$P({X=3})={({\frac{1}{4}})^3}=\frac{1}{64}$.
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
点评 本题考查了古典概率计算公式与相互对立事件的概率计算公式、二项分布列的计算公式与数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知x>0,y>0且x+y=xy,则x+y的取值范围是( )
| A. | (0,1] | B. | [2,+∞) | C. | (0,4] | D. | [4,+∞) |
1.下列函数为奇函数的是( )
| A. | y=x2+1 | B. | y=x3-2x | C. | y=2x+1 | D. | y=2x4+3x2 |
15.若$sin({x+\frac{π}{6}})=\frac{1}{3}$,则$tan({2x+\frac{π}{3}})$等于( )
| A. | $\frac{7}{9}$ | B. | $±\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{7}$ | D. | $±\frac{{4\sqrt{2}}}{7}$ |
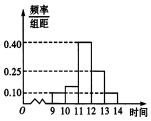 在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )
在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )