题目内容
5.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2+2x,若f(2-a2)>f(a2),则实数a的取值范围是(-1,1).分析 题意可先判断出f(x)=x2+2x=(x+1)2-1在(0,+∞)上单调递增,根据偶函数的对称区间上的单调性可知,f(x)在(-∞,0)上单调递减,从而可比较2-a2与a2的大小,解不等式可求a的范围.
解答 解:∵f(x)=x2+2x=(x+1)2-1在(0,+∞)上单调递增,
又∵f(x)是定义在R上的偶函数,
根据偶函数的对称区间上的单调性可知,f(x)在(-∞,0)上单调递减,
∵f(2-a2)>f(a2),
∴|2-a2|>a2,
解不等式可得,-1<a<1,
故答案为:(-1,1)
点评 本题主要考查了偶函数在对称区间上的单调性相反(奇函数对称区间上的单调性相同)的性质的应用,一元二次不等式的求解,属于中档题.

练习册系列答案
相关题目
16.在圆x2+y2=4上,与直线 l:4x+3y-12=0的距离最大的点的坐标是( )
| A. | $({\frac{8}{5},\frac{6}{5}})$ | B. | $({\frac{8}{5},-\frac{6}{5}})$ | C. | $({-\frac{8}{5},-\frac{6}{5}})$ | D. | $({-\frac{8}{5},\frac{6}{5}})$ |
 某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):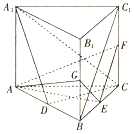 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F、G分别是BC、CC1、BB1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F、G分别是BC、CC1、BB1的中点.