题目内容
18.函数$f(x)=\left\{\begin{array}{l}{e^{x+3}},x<0\\ \sqrt{-{x^2}+2x},0≤x≤2\end{array}\right.$若g(x)=f(x)-kx-2k恰有两个两点,则实数k的取值范围为$({e^2},\frac{e^3}{2})∪[0,\frac{{\sqrt{2}}}{4})$.分析 由题意可得,f(x)=k(x+2)有两个不等的实根,作出y=f(x)的图象和直线y=k(x+2),通过图象观察它们有两个交点的情况,注意运用导数求切线的斜率和直线和圆相切的条件:d=r
解答 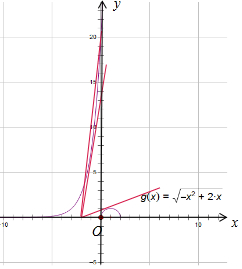 解:函数g(x)=f(x)-kx-2k恰有两个零点,
解:函数g(x)=f(x)-kx-2k恰有两个零点,
即为f(x)=k(x+2)有两个不等的实根,如图:
当x<0时,直线和曲线相切,设切点为(m,km+2k),
f′(x)=ex+3,f′(m)=em+3,
由em+3=km+2k,k,k≠0,解得k=e2,m=-1,
k<$\frac{{e}^{3}}{2}$,
当直线经过点(0,e3),k=$\frac{{e}^{-3}}{2}$时,直线和曲线有两个交点,
当直线kx-y+2k=0和半圆相切,d=r=1,圆心为(1,0),
由$\frac{|3k|}{\sqrt{{k}^{2}+1}}$=1,解得k=$\frac{\sqrt{2}}{4}$(负的舍去),
由图象可得,0≤k≤$\frac{\sqrt{2}}{4}$时,直线和半圆有两个交点.
则有k的取值范围是:[0,$\frac{\sqrt{2}}{4}$)∪[e2,$\frac{{e}^{3}}{2}$).
故答案为:[0,$\frac{\sqrt{2}}{4}$)∪[e2,$\frac{{e}^{3}}{2}$).
点评 本题考查函数的零点的求法,主要考查函数和方程的转化思想,运用数形结合的思想方法是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.已知命题p:函数f(x)=$\frac{2x+3}{x}$图象的对称中心为(0,3);命题q:若单位向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|2$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+2$\overrightarrow{b}$|,则2$\overrightarrow{a}$⊥3$\overrightarrow{b}$,则下列命题是真命题的为( )
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
9.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的两个焦点分别为F1,F2,以线段F1F2为直径的圆与双曲线渐近线一个交点为(4,3),则该双曲线的实轴长为( )
| A. | 6 | B. | 8 | C. | 4 | D. | 10 |
8.在等差数列{an}中,a1=3,2a2=a4,则a7等于( )
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
 某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):