题目内容
如果点M(x,y)在运动过程中,总满足关系式
-
=6,点M的轨迹方程为 .(要求方程化为最简形式)
| (x-4)2+y2 |
| (x+4)2+y2 |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:
-
=6,表示点M(x,y)与定点(4,0),(-4,0)的距离的差为6,利用双曲线的定义,即可得到结论.
| (x-4)2+y2 |
| (x+4)2+y2 |
解答:
解:
-
=6,表示点M(x,y)与定点(4,0),(-4,0)的距离的差为6,
∵6<8
∴点M(x,y)的轨迹是以(±4,0)为焦点,实轴长为6的双曲线的左支,
∵2a=6,c=4
∴b=
∴点M的轨迹方程为
-
=1(x≤-3).
故答案为:
-
=1(x≤-3).
| (x-4)2+y2 |
| (x+4)2+y2 |
∵6<8
∴点M(x,y)的轨迹是以(±4,0)为焦点,实轴长为6的双曲线的左支,
∵2a=6,c=4
∴b=
| 7 |
∴点M的轨迹方程为
| x2 |
| 9 |
| y2 |
| 7 |
故答案为:
| x2 |
| 9 |
| y2 |
| 7 |
点评:本题考查双曲线的轨迹方程,解题的关键是掌握双曲线的定义,属于基础题.

练习册系列答案
相关题目
在等差数列{an}中,若a1+a4+a7=45,a2+a5+a8=39,则a3+a6+a9=( )
| A、33 | B、30 | C、27 | D、24 |
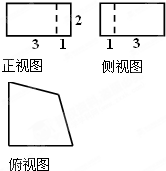
 已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中面积最大值是
已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中面积最大值是