题目内容

18．等差数列{an}中，a4+a7=22．则数列{an}的前10项和等于（　　）
A．220B．110C．55D．100

分析 利用等差数列的性质，之间求解数列的和即可．

解答 解：等差数列{an}中，a4+a7=22．则数列{an}的前10项和为：$\frac{10（{a}_{1}+{a}_{10}）}{2}$=$\frac{10×（{a}_{4}+{a}_{7}）}{2}$=$\frac{10×22}{2}$=110．
故选：B．

点评 本题考查数列的性质的应用，等差数列求和，考查计算能力．

练习册系列答案
相关题目
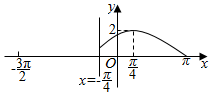8．已知定义在区间[-$\frac{3π}{2}$，π]上的函数y=f（x）的图象关于直线x=-$\frac{π}{4}$对称，当x∈[-$\frac{π}{4}$，π]时，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$），且其图象如图所示．
（1）求函数y=f（x）在区间[-$\frac{3π}{2}$，π]上的表达式；
（2）求满足f（x）=$\sqrt{3}$的实数x的集合．
9．若x＞1，y＞$\frac{1}{2}$，不等式$\frac{{x}^{2}}{a（2y-1）}$+$\frac{4{y}^{2}}{a（x-1）}$≥1恒成立，则实数a的最大值是（　　）
A．8B．4C．2$\sqrt{2}$D．$\sqrt{2}$
6．已知各项均为正数的数列{an}的前n项和为Sn，且2$\sqrt{{S}_{n}}$=an+1．
（I）求数列{an}的通项公式．
（Ⅱ）设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$，数列{bn}的前n项和为Tn，若对任意n∈N*，λ＞Tn都成立，求实数λ的取值范围．
13．若等差数列中，有a1+a5=5，则2a2+3a3+a5=15．
3．①从甲、乙、丙3名同学中选出2名分别去参加两个乡镇的社会调查，有多少种不同的选法？
②有4张电影票，要在7人中确定4人去观看，有多少种不同的选法？
③某人射击8枪，击中4枪，且命中的4枪均为2枪连中，则不同的结果有多少种？
其中组合问题的个数是（　　）
A．0B．1C．2D．3
10．已知数列{an}中，a1=1，若2an+1-an=$\frac{n-2}{n（n+1）（n+2）}$，bn=an-$\frac{1}{n（n+1）}$．
（1）求证：{bn}为等比数列，并求出{an}的通项公式；
（2）若Cn=nbn+$\frac{1}{n（n+1）}$，且其前n项和为Tn，求证：Tn＜3．
7．已知三个共线向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$的坐标分别为$\overrightarrow{a}$=（2，-1）、$\overrightarrow{b}$=（x，2）、$\overrightarrow{c}$=（-3，y），且实数x+y的值等于-$\frac{5}{2}$．
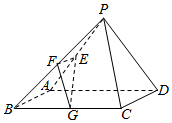10．已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E，F，G分别是PA，PB，BC的中点．
（Ⅰ）求证：EF⊥平面PAD；（Ⅱ）求平面EFG与平面ABCD所成锐二面角的大小；
（Ⅲ）线段PD上是否存在一个动点M，使得直线GM与平面EFG所成角为$\frac{π}{6}$，若存在，求线段PM的长度，若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网