题目内容
6.已知各项均为正数的数列{an}的前n项和为Sn,且2$\sqrt{{S}_{n}}$=an+1.(I)求数列{an}的通项公式.
(Ⅱ)设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,数列{bn}的前n项和为Tn,若对任意n∈N*,λ>Tn都成立,求实数λ的取值范围.
分析 (I)化简可得4Sn=(an+1)2,从而分类讨论可判断数列{an}是以1为首项,2为公差的等差数列,从而解得;
(Ⅱ)由(I)知,bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),从而利用裂项求其前n项和,化恒成立问题为最值问题.
解答 解:(I)∵2$\sqrt{{S}_{n}}$=an+1,
∴4Sn=(an+1)2,
当n=1时,4a1=(a1+1)2,
解得,a1=1;
当n≥2时,4Sn=(an+1)2,4Sn-1=(an-1+1)2,
故4an=(an+1)2-(an-1+1)2,
化简可得,
(an+an-1)(an-an-1-2)=0,
∵an>0,
∴an-an-1-2=0,
故数列{an}是以1为首项,2为公差的等差数列,
故其通项公式为an=1+2(n-1)=2n-1;
(Ⅱ)由(I)知,
bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
故Tn=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$<$\frac{1}{2}$,
故若对任意n∈N*,λ>Tn都成立,
则λ≥$\frac{1}{2}$.
点评 本题考查了等差数列的判断与应用,同时考查了分类讨论的思想应用及恒成立问题与最值问题的应用,同时考查了裂项求和法的应用.

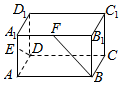 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | 220 | B. | 110 | C. | 55 | D. | 100 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 1 | B. | -1 | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |