题目内容
下列角中终边与390°相同的角是（ ）
| A、30° | B、-30° |
| C、630° | D、-630° |
考点：终边相同的角
专题：三角函数的求值
分析：根据终边相同的角之间相差周角的整数倍，可以表示出与390°的角终边相同的角α的集合，分析题目中的四个答案，找出是否存在满足条件的k值，即可得到答案．
解答：
解：∵与390°的角终边相同的角α的集合为
{α|α=390°+k•360°，k∈Z}
当k=-1时，α=30°
故选：A．
{α|α=390°+k•360°，k∈Z}
当k=-1时，α=30°
故选：A．
点评：本题考查的知识点是终边相同的角，其中根据终边相同的角之间相差周角的整数倍，表示出与390°的角终边相同的角α的集合，是解答本题的关键．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
已知向量
，
，
均为单位向量，且
⊥
，向量
，
与
的夹角分别为
，
，则|
+
+
|=（ ）
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| c |
| π |
| 4 |
| 3π |
| 4 |
| a |
| b |
| c |
A、
| ||
| B、2 | ||
C、1+
| ||
| D、1 |
如图，已知
=
，则（ ）
| AB |
| 1 |
| 3 |
| AP |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
点P（x，y）在直线x+y-2=0上，则P到原点距离的最小值是（ ）
A、2
| ||
B、
| ||
| C、1 | ||
| D、2． |
若直线经过点P（1，1）和点Q（2，t+
），其中t＞0，则该直线的倾斜角的取值范围是（ ）
| 1 |
| t |
A、（0，
| ||||
B、[
| ||||
C、（
| ||||
D、[
|
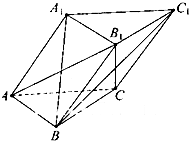已知三棱柱ABC-A1B1C1中，底面边长和侧棱长均为a，侧面A1ACC1⊥底面ABC，A1B=