题目内容
函数f1(x)=cosx﹣sinx,记f2(x)=f1′(x),f3(x)=f2′(x),…fn(x)=fn﹣1′(x),(n∈N*,n≥2),则 =( )
=( )
A.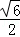 B.
B.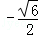 C.0 D.2008
C.0 D.2008
B
【解析】
试题分析:先求出f2(x)、f3(x)、f4(x),观察所求的结果,归纳其中的周期性规律,求解即可.
【解析】
由题意,f2(x)=f1′(x)=﹣sinx﹣cosx
f3(x)=f2′(x)=﹣cosx+sinx,
f4(x)=(﹣cosx+sinx)′=sinx+cosx,
f5(x)=cosx﹣sinx,
以此类推,可得出fn(x)=fn+4(x)
又∵f1(x)+f2(x)+f3(x)+f4(x)=0,
∴ =
= =﹣
=﹣ .
.
故选B.

练习册系列答案
相关题目
 的导数为( )
的导数为( )



 B.
B. C.
C. D.
D.
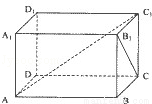
 = .
= .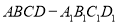 棱长为4,点
棱长为4,点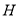 在棱
在棱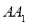 上,且
上,且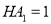 .在侧面
.在侧面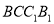 内作边长为1的正方形
内作边长为1的正方形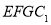 ,
,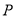 是侧面
是侧面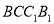 内一动点,且点
内一动点,且点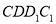 距离等于线段
距离等于线段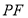 的长.则当点
的长.则当点 运动时,
运动时,  的最小值是 ( )
的最小值是 ( )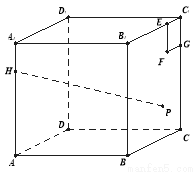
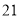 (B)
(B) (C)
(C) (D)
(D)