题目内容
5.函数y=sin2x的单调减区间是( )| A. | $[\frac{π}{2}+2kπ,\frac{3}{2}π+2kπ](k∈Z)$ | B. | $[kπ+\frac{π}{4},kπ+\frac{3}{4}π](k∈Z)$ | ||
| C. | [π+2kπ,3π+2kπ](k∈Z) | D. | $[kπ-\frac{π}{4},kπ+\frac{π}{4}](k∈Z)$ |
分析 结合正弦函数的单调性即可得到结论.
解答 解:∵y=sinx的单调减区间为[2kπ$+\frac{π}{2}$,2kπ+$\frac{3π}{2}$],
∴2x∈[2kπ$+\frac{π}{2}$,2kπ+$\frac{3π}{2}$],即2kπ$+\frac{π}{2}$≤2x≤2kπ+$\frac{3π}{2}$,k∈Z.
解得:kπ$+\frac{π}{4}$≤x≤kπ+$\frac{3π}{4}$,k∈Z.
∴函数y=sin2x的单调减区间是[kπ$+\frac{π}{4}$,kπ+$\frac{3π}{4}$],
故选:B.
点评 本题主要考查三角函数的图象和性质,单调性的运用.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.平面截球得到的半径是3的圆面,球心到这个平面的距离是4,则该球的表面积是( )
| A. | 20π | B. | $\frac{416\sqrt{3}π}{3}$ | C. | $\frac{500π}{3}$ | D. | 100π |
15.设△ABC的内角A、B、C的对边分别为a、b、c,若a=1,c=$\sqrt{3}$,cosA=$\frac{\sqrt{3}}{2}$,且b<c,则b=( )
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
 某班级将从甲、乙两位同学中选派一人参加数学竞赛,老师对他们平时的5次模拟测试成绩(满分:100分)进行了记录,其统计数据的茎叶图如图所示,已知甲、乙两位同学的平均成绩都为90分.
某班级将从甲、乙两位同学中选派一人参加数学竞赛,老师对他们平时的5次模拟测试成绩(满分:100分)进行了记录,其统计数据的茎叶图如图所示,已知甲、乙两位同学的平均成绩都为90分.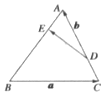 如图,△ABC中,$\frac{CD}{DA}=\frac{AE}{EB}=\frac{1}{2}$,记$\overrightarrow{BC}=\overrightarrow{a,}\overrightarrow{CA}=\overrightarrow b$,则$\overrightarrow{DE}$=$\frac{1}{3}(\overrightarrow b-\overrightarrow a)$.(用$\overrightarrow a$和$\overrightarrow b$表示)
如图,△ABC中,$\frac{CD}{DA}=\frac{AE}{EB}=\frac{1}{2}$,记$\overrightarrow{BC}=\overrightarrow{a,}\overrightarrow{CA}=\overrightarrow b$,则$\overrightarrow{DE}$=$\frac{1}{3}(\overrightarrow b-\overrightarrow a)$.(用$\overrightarrow a$和$\overrightarrow b$表示)