题目内容
设函数f(x)=log a2-1(2x+1)在区间(-
,0)上恒有f(x)>0.
(1)求a的取值范围,
(2)判断f(x)的增减性.
| 1 |
| 2 |
(1)求a的取值范围,
(2)判断f(x)的增减性.
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:(1)由(-
,0)可得2x+1∈(0,1),从而求a的取值范围;
(2)由复合函数的单调性判断函数的单调性.
| 1 |
| 2 |
(2)由复合函数的单调性判断函数的单调性.
解答:
解:(1)∵x∈(-
,0),
∴2x+1∈(0,1),
故由函数f(x)=log a2-1(2x+1)在区间(-
,0)上恒有f(x)>0得,
0<a2-1<1;
解得1<a<
或-
<a<-1;
(2)由复合函数的单调性可知,
函数f(x)=log a2-1(2x+1)在其定义域(-
,+∞)上是减函数.
| 1 |
| 2 |
∴2x+1∈(0,1),
故由函数f(x)=log a2-1(2x+1)在区间(-
| 1 |
| 2 |
0<a2-1<1;
解得1<a<
| 2 |
| 2 |
(2)由复合函数的单调性可知,
函数f(x)=log a2-1(2x+1)在其定义域(-
| 1 |
| 2 |
点评:本题考查了对数函数的性质及复合函数的单调性的应用,属于基础题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
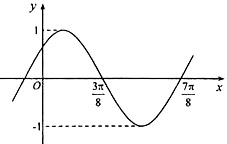 已知函数y=sin(ωx+φ)(ω>0,|φ|<
已知函数y=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
A、y=sin(2x+
| ||
B、y=sin(2x+
| ||
C、y=sin(4x+
| ||
D、y=sin(4x+
|