题目内容
不等式
>
的解集为 .
| 1 |
| 4x-1 |
| 1 |
| 2x-3 |
考点:指、对数不等式的解法
专题:不等式的解法及应用
分析:把已知的分式不等式移向,化为
<0,由22x-2x+2>0得(2x+1)(2x-1)(2x-3)<0,穿根后求出1<2x<3.然后求解指数不等式得答案.
| 22x-2x+2 |
| (2x+1)(2x-1)(2x-3) |
解答:
解:由
>
,得
-
>0,
即
>0,也就是
<0,
∵22x-2x+2>0,
∴(2x+1)(2x-1)(2x-3)<0,
由穿根法可得:2x<-1(舍)或1<2x<3.
解得0<x<log23.
∴不等式
>
的解集为(0,log23).
故答案为:(0,log23).
| 1 |
| 4x-1 |
| 1 |
| 2x-3 |
| 1 |
| 4x-1 |
| 1 |
| 2x-3 |
即
| 2x-3-22x+1 |
| (22x-1)(2x-3) |
| 22x-2x+2 |
| (2x+1)(2x-1)(2x-3) |
∵22x-2x+2>0,
∴(2x+1)(2x-1)(2x-3)<0,
由穿根法可得:2x<-1(舍)或1<2x<3.
解得0<x<log23.
∴不等式
| 1 |
| 4x-1 |
| 1 |
| 2x-3 |
故答案为:(0,log23).
点评:本题考查了分式不等式和指数不等式的解法,训练了穿根法求解高次不等式,是中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知函数f(x)=
是x∈(-∞,+∞)上的减函数,则a的取值范围是( )
|
A、(0,
| ||||
B、(
| ||||
| C、(2,3) | ||||
D、(
|
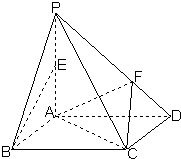 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,E为PA的中点.
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,E为PA的中点.