题目内容
某曲线y=f（x）在x=5处的切线方程为y=-x+8，则f（5）+f′（5）=（ ）
| A、6 | B、2 | C、4 | D、-2 |
考点：利用导数研究曲线上某点切线方程,导数的运算
专题：导数的综合应用
分析：求出函数的导数，根据导数的几何意义即可得到结论．
解答：
解：∵曲线y=f（x）在x=5处的切线方程为y=-x+8，
∴f′（5）=-1，
当x=5时，y=-5+8=3，即f（5）=3，
则f（5）+f′（5）=3-1=2，
故选：B．
∴f′（5）=-1，
当x=5时，y=-5+8=3，即f（5）=3，
则f（5）+f′（5）=3-1=2，
故选：B．
点评：本题主要考查导数的几何意义，函数的切线将提供切线斜率和切点坐标，比较基础．
练习册系列答案
相关题目
阅读如图所示的程序框图，它的输出结果是（ ）
| A、0 | ||
B、
| ||
| C、π | ||
D、1+
|
若关于x的不等式|x-1|+|x-4|＜a的解集为空集，则a的取值范围为（ ）
| A、a≥3 | B、a≤3 |
| C、a≥5 | D、a≤5 |
在△ABC中，a=2
，b=2
，B=
，则A等于（ ）
| 3 |
| 2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中，角A、B、C的对边分别为a、b、c，且b+c=2ccos2
，则△ABC是（ ）
| A |
| 2 |
| A、直角三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
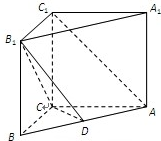已知直三棱柱ABC-A1B1C1中，AC=BC=AA1=4，AC⊥BC，若D是AB中点．