题目内容
在△ABC中，角A、B、C的对边分别为a、b、c，且b+c=2ccos2
，则△ABC是（ ）
| A |
| 2 |
| A、直角三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
考点：三角形的形状判断,正弦定理
专题：解三角形
分析：首先根据二倍角公式化简所给的式子，然后余弦定理可知cosA=
，代入化简后的式子，即可得出答案．
| b2+c2-a2 |
| 2bc |
解答：
解：∵2ccos2
=2c（
）=c+ccosA=b+c，∴cosA=
．
∵在△ABC中，cosA=
，∴
=
整理得：c2=a2+b2 故ABC为直角三角形，
故选：A．
| A |
| 2 |
| 1+cosA |
| 2 |
| b |
| c |
∵在△ABC中，cosA=
| b2+c2-a2 |
| 2bc |
| b2+c2-a2 |
| 2bc |
| b |
| c |
整理得：c2=a2+b2 故ABC为直角三角形，
故选：A．
点评：本题主要考查了二倍角公式和余弦定理的运用，熟练掌握公式和定理是解题的关键，属于基础题．
练习册系列答案
相关题目
已知△ABC中，角A、B、C所对的边分别是a、b、c；且a=1，b=2，C=150°，则△ABC的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知等差数列{an}中，a3+a8=22，a6=7，则a5的值为（ ）
| A、5 | B、15 | C、20 | D、25 |
设a＞0，b＞0，则“a2+b2≤1”是“a+b≤ab+1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
某曲线y=f（x）在x=5处的切线方程为y=-x+8，则f（5）+f′（5）=（ ）
| A、6 | B、2 | C、4 | D、-2 |
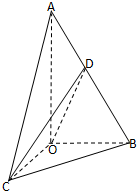如图，在三棱锥A-BOC中，∠OAB=30°，AO⊥平面BOC，AB=4，∠BOC=90°，BO=CO，D是AB的中点．
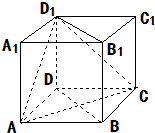如图，在正方体ABCD-A1B1C1D1中．求证：平面ACD1⊥平面BB1D1D．
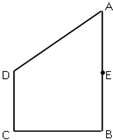如图所示，在直角梯形ABCD中，E是AB的中点，∠B=∠C=90°，