题目内容
17.直线x-y-2=0 与x-y+1=0之间的距离是$\frac{{3\sqrt{2}}}{2}$.分析 根据两条平行直线间的距离公式,即可求得结论.
解答 解:根据两条平行直线间的距离公式可得d=$\frac{|1+2|}{\sqrt{2}}$=$\frac{{3\sqrt{2}}}{2}$.
故答案为:$\frac{{3\sqrt{2}}}{2}$.
点评 本题考查两条平行直线间的距离公式的运用,考查计算能力,属于基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
12.已知集合A={x∈R|-1<x<3},B={x∈R|-1<x<m+1},若x∈B成立的一个充分不必要条件是x∈A,则实数m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | -2<m<2 |
2.若集合M={-1,0,1,2},N={0,2,4,6},则M∩N=( )
| A. | {-1,1,6} | B. | {-1,1} | C. | {-1,0,1,2,4,6} | D. | {0,2} |
9.随机变量ξ的分布列如表,则D(ξ)=$\frac{5}{9}$
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | p |
6.“x2-2x<0”是“log2(2-x)<2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
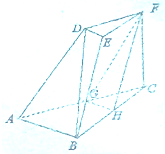 如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.