题目内容
16.已知动点P(x,y)满足$2\sqrt{{{(x-3)}^2}+{{(y+2)}^2}}=|{2x+y-5}|$,则点P的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
分析 利用圆锥曲线的第二定义,转化求解即可.
解答 解:动点P(x,y)满足$2\sqrt{{{(x-3)}^2}+{{(y+2)}^2}}=|{2x+y-5}|$,
可得:$\frac{\sqrt{(x-3)^{2}+(y+2)^{2}}}{\frac{|2x+y-5|}{\sqrt{5}}}=\frac{\sqrt{5}}{2}>1$,
就是动点到定点(3,-2)的距离与到定直线2x+y-5=0的距离的比是常数$\frac{\sqrt{5}}{2}$,满足双曲线的第二定义,
所求轨迹是双曲线.
故选:C.
点评 本题考查双曲线的第二定义的应用,轨迹方程的判断,是基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.在同一平面直角坐标系中,点A($\frac{1}{3}$,-2)经过伸缩变换φ:$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$所得的点A′的坐标为( )
| A. | (1,-1) | B. | (1,-4) | C. | $({\frac{1}{9},-4})$ | D. | (9,-1) |
4.已知点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右顶点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,椭圆上的点到点M的距离d的最小值( )
| A. | $\frac{4\sqrt{3}}{5}$ | B. | $\sqrt{15}$ | C. | -1 | D. | 1 |
6.命题?x∈R,tanx≠1,的否定是( )
| A. | ?x∉R,tanx≠1 | B. | ?x∈R,tanx=1 | C. | ?x0∉Rtanx0=1 | D. | ?x0∈R,tanx0=1 |
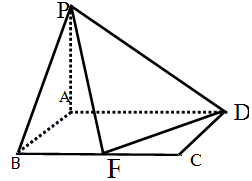 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点