题目内容
11．某几何体的三视图如图所示，则它的表面积为$\frac{5+\sqrt{5}}{2}$，体积为$\frac{π}{3}$．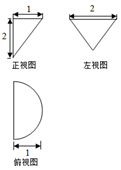
分析 由已知中的三视图，可得该几何体是一个以俯视图为底面的半圆锥，代入半圆锥体积和表面积公式，可得答案．
解答 解：由已知中的三视图，可得该几何体是一个以俯视图为底面的半圆锥，
半圆锥的底面直径为2，高h=2，
故半圆锥的底面半径r=1，母线长为$\sqrt{5}$，
故半圆锥的体积V=$\frac{1}{2}×$$\frac{1}{3}{πr}^{2}h$=$\frac{π}{3}$，
半圆锥的表面积S=$\frac{1}{2}$×2×2+$\frac{1}{2}$（1+$\sqrt{5}$）π=$\frac{5+\sqrt{5}}{2}$π
故答案为：$\frac{5+\sqrt{5}}{2}$π，$\frac{π}{3}$
点评 本题考查的知识点半圆锥的体积和表面积，空间几何体的三视图．
练习册系列答案
相关题目
2．在同一平面直角坐标系中，点A（$\frac{1}{3}$，-2）经过伸缩变换φ：$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$所得的点A′的坐标为（ ）
| A． | （1，-1） | B． | （1，-4） | C． | $（{\frac{1}{9}，-4}）$ | D． | （9，-1） |
19．某空间几何体的三视图如图所示，则该几何体的体积是（ ）
| A． | 32 | B． | 32$\sqrt{2}$ | C． | $\frac{32}{3}$ | D． | $\frac{32}{3}$$\sqrt{2}$ |
16．
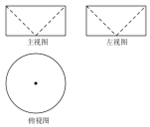如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的表面积为（ ）
如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的表面积为（ ）| A． | （$\sqrt{2}$+1）π | B． | （$\sqrt{2}$+2）π | C． | （$\sqrt{2}$+3）π | D． | （$\sqrt{2}$+4）π |
4．已知点A，B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右顶点，点F是椭圆的右焦点，点P在椭圆上，且位于x轴上方，PA⊥PF．设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，椭圆上的点到点M的距离d的最小值（ ）
| A． | $\frac{4\sqrt{3}}{5}$ | B． | $\sqrt{15}$ | C． | -1 | D． | 1 |