题目内容
现有6本不同的教科书，语文、数学、英语各2本，需将它们在书架上摆成一排（不叠放），其中语文书必须摆在两端，且两本数学书相邻，则不同摆法的种数为（ ）
| A、12 | B、18 | C、24 | D、36 |
考点：排列、组合及简单计数问题
专题：排列组合
分析：利用分布计数原理，第一步先排英语，第二步排数学，第三步排语文，问题得以解决
解答：
解：分三步，第一步先排英语，第二步，排完英语后形成了3个间隔，任选2个间隔插入数学，第三步在两端插入语文，根据分步计数原理得
•
=24种．
故选：C．
| A | 2 2 |
| •A | 2 3 |
| A | 2 2 |
故选：C．
点评：本题主要考查了分步计数原理，不相邻问题用“插空”，特殊元素、特殊位置优先考虑的原则．
练习册系列答案
相关题目
若两个平面互相平行，则分别在这两个平行平面内的两条直线（ ）
| A、平行 | B、异面 |
| C、相交 | D、平行或异面 |
已知函数f（x）=（1-2x3）6，则f′（1）等于（ ）
| A、0 | B、-6 | C、-36 | D、36 |
关于x的不等式x2-ax-6a2＜0（a＞0）的解集为（x1，x2），且x2-x1=10，则a=（ ）
| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
若f（x）=sinx+cos5，则该函数在点（5，f（5））处切线的斜率等于（ ）
| A、sin5+cos5 |
| B、cos5 |
| C、sin5 |
| D、sin5-cos5 |
若点O和点F分别为椭圆
+y2=1的中心和左焦点，点P为椭圆上的任意一点，则
•
的最大值为（ ）
| x2 |
| 2 |
| OP |
| FP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
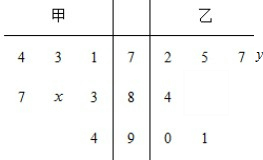某中学高二年级的甲、乙两个班中，需根据某次数学预赛成绩选出某一班的7名学生参加数学竞赛决赛，已知这次预赛他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班7名学生成绩的平均分是81，乙班7名学生成绩的中位数是78．