题目内容
13.若实数a+b=2,a>0,b>0,则$\frac{1}{a}+\frac{a}{b}$的最小值为$\frac{1}{2}+\sqrt{2}$.分析 实数a+b=2,a>0,b>0,则$\frac{1}{a}+\frac{a}{b}$=$\frac{1}{2}\frac{a+b}{a}$+$\frac{a}{b}$=$\frac{1}{2}$+$\frac{b}{2a}$+$\frac{a}{b}$,利用基本不等式的性质即可得出.
解答 解:∵实数a+b=2,a>0,b>0,
则$\frac{1}{a}+\frac{a}{b}$=$\frac{1}{2}\frac{a+b}{a}$+$\frac{a}{b}$=$\frac{1}{2}$+$\frac{b}{2a}$+$\frac{a}{b}$≥$\frac{1}{2}$+2$\sqrt{\frac{b}{2a}•\frac{a}{b}}$=$\frac{1}{2}$+$\sqrt{2}$,当且仅当b=$\sqrt{2}$a=4-2$\sqrt{2}$时取等号.
故答案为:$\frac{1}{2}+\sqrt{2}$.
点评 本题考查了变形利用基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.若一段圆弧的长度等于该圆内接正三角形的边长,则这段弧所对圆心角弧度为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
2.k∈Z时,$\frac{sin(kπ-α)•cos(kπ+α)}{sin[(k+1)π+α]•cos[(k+1)π+α]}$的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 与α取值有关 |
3.设数列{an}的前n项和${S_n}=\frac{n}{n+2}$,则a6的值为( )
| A. | $-\frac{1}{28}$ | B. | $-\frac{1}{56}$ | C. | $\frac{1}{28}$ | D. | $\frac{1}{56}$ |
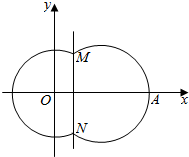 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).