题目内容
20.设函数$f(x)=cos({πx-π})+1,\;\;x∈({\frac{1}{2},\frac{3}{2}})$,若关于x的方程2[f(x)]2-(2a+3)f(x)+3a=0有四个不同的实数解,则满足题意的实数a的取值范围是( )| A. | (0,1) | B. | $({0,\frac{3}{2}})$ | C. | (1,2) | D. | $({1,\frac{3}{2}})∪({\frac{3}{2},2})$ |
分析 化简方程可得f(x)=$\frac{3}{2}$或f(x)=a;从而作函数$f(x)=cos({πx-π})+1,\;\;x∈({\frac{1}{2},\frac{3}{2}})$的图象,化为图象的交点的个数问题即可.
解答 解:∵2[f(x)]2-(2a+3)f(x)+3a=0,
∴(2f(x)-3)(f(x)-a)=0,
∴f(x)=$\frac{3}{2}$或f(x)=a;
作函数$f(x)=cos({πx-π})+1,\;\;x∈({\frac{1}{2},\frac{3}{2}})$的图象如下,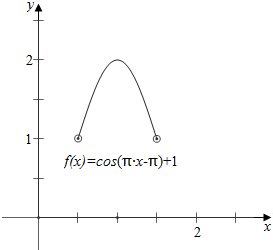 ,
,
结合图象可知,
1<a<$\frac{3}{2}$或$\frac{3}{2}$<a<2;
故选:D.
点评 本题考查了方程的根的解法及数形结合的思想应用,同时考查了转化思想的应用.

练习册系列答案
相关题目
8.角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,则角α与角180°+α的终边关系为( )
| A. | 一定关于x轴对称 | B. | 一定关于y轴对称 | C. | 关于原点对称 | D. | 不具有对称性 |
11.某地最近十年粮食需求量逐年上升,如表是部分统计数据:
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程y=bx+a;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
提示:线性回归方程y=a+bx,$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$.
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
提示:线性回归方程y=a+bx,$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$.
12.下列说法中,正确的是( )
| A. | 幂函数的图象都经过点(1,1)和点(0,0) | |
| B. | 当α=0时,函数y=xα的图象是一条直线 | |
| C. | 若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大 | |
| D. | 幂函数y=xα,当α<0时,在第一象限内函数值随x值的增大而减小 |
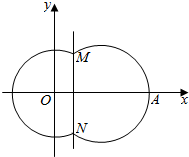 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0). 某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示.