题目内容
2．已知F1，F2是椭圆$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1的两个焦点，过点F2的直线交椭圆于M，N两点，在△F1MN中，若有两边之和是14，则第三边的长度为（ ）| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
分析 由椭圆性质得在△F1MN中，|F1M|+|F1N|+|MN|=4a，由此能求出第三边的长度．
解答 解：∵F1，F2是椭圆$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1的两个焦点，过点F2的直线交椭圆于M，N两点，
∴在△F1MN中，|F1M|+|F1N|+|MN|=4a=20，
∵在△F1MN中有两边之和是14，
∴第三边的长度为：20-14=6．
故选：A．
点评 本题考查椭圆中第三边的长度的求法，是基础题，解题时要认真审题，注意椭圆性质的合理运用．
练习册系列答案
相关题目
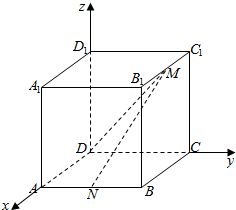在长方体ABCD-A1B1C1D1中，|AB|=|BC|=2，|D1D|=3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系．
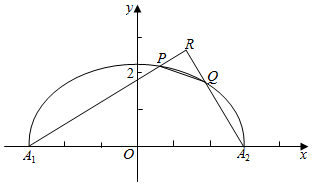如图，设P是上半椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（y≥0）上任意一点，F为右焦点，PF的最小值是$\sqrt{2}$-1，离心率是$\frac{\sqrt{2}}{2}$，上半椭圆C与x轴交于点A1，A2．
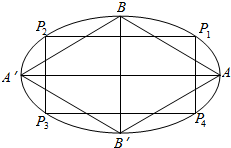如图，在椭圆中，A′A，B′B分别是长轴，短轴，P1P2P3P4是各边皆平行于对称轴的内接矩形，四边形A′B′AB，P1P2P3P4的面积分别记作Q，S．求证：S≤Q．
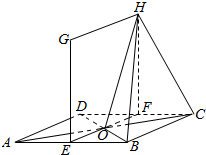如图，菱形ABCD中，∠BAD=60°，边长AB=2，GE⊥平面ABCD，EF⊥ABCD，E，F分别是边AB、CD中点，AC与BD交于O，EG=FH=2，