题目内容
7.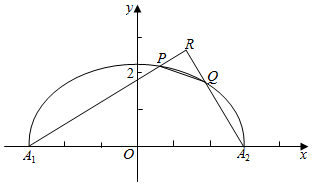 如图,设P是上半椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(y≥0)上任意一点,F为右焦点,PF的最小值是$\sqrt{2}$-1,离心率是$\frac{\sqrt{2}}{2}$,上半椭圆C与x轴交于点A1,A2.
如图,设P是上半椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(y≥0)上任意一点,F为右焦点,PF的最小值是$\sqrt{2}$-1,离心率是$\frac{\sqrt{2}}{2}$,上半椭圆C与x轴交于点A1,A2.(1)求出a2,b2的值;
(2)设P是上半椭圆C上位于第一象限内的任意一点,过A2作A2R⊥A1P于R,设A2R与曲线C交于Q,求直线PQ斜率的取值范围.
分析 (1)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,PF的最小值为a-c=$\sqrt{2}$-1,解方程可得a,c,由a,b,c的关系即可得到b,可得所求值;
(2)先考察一般性,直线A1P的方程是y=k(x+a),与椭圆方程联立,求得P,Q的坐标,可得直线PQ斜率,即可求出取值范围.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
PF的最小值为a-c=$\sqrt{2}$-1,
解得a=$\sqrt{2}$,c=1,b=1,
即有a2=2,b2=1;
(2)为了减少计算量,先考察一般性.
设曲线C的方程是$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≥0),直线A1P的斜率是k,
因为P是曲线C上位于第一象限内的任意一点,所以k∈(0,$\frac{b}{a}$),
设P,Q的坐标分别是(x1,y1),(x2,y2),则直线A1P的方程是y=k(x+a),
由$\left\{\begin{array}{l}{y=k(x+a)}\\{{b}^{2}{x}^{2}+{a}^{2}{y}^{2}={a}^{2}{b}^{2}}\end{array}\right.$消去y得,
(a2k2+b2)x2+2a3k2x+a2(a2k2-b2)=0,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{a({b}^{2}-{a}^{2}{k}^{2})}{{b}^{2}+{a}^{2}{k}^{2}}}\\{{y}_{1}=\frac{2a{b}^{2}k}{{b}^{2}+{a}^{2}{k}^{2}}}\end{array}\right.$.
将上式中的a换成-a,k换成-$\frac{1}{k}$得$\left\{\begin{array}{l}{{x}_{2}=\frac{a({a}^{2}-{b}^{2}{k}^{2})}{{a}^{2}+{b}^{2}{k}^{2}}}\\{{y}_{2}=\frac{2a{b}^{2}k}{{a}^{2}+{b}^{2}{k}^{2}}}\end{array}\right.$.
又上式中的a=$\sqrt{2}$,b=1,代入可解得$\left\{\begin{array}{l}{{x}_{1}=\frac{\sqrt{2}(1-2{k}^{2})}{1+2{k}^{2}}}\\{{y}_{1}=\frac{2\sqrt{2}k}{1+2{k}^{2}}}\end{array}\right.$,
$\left\{\begin{array}{l}{{x}_{2}=\frac{\sqrt{2}(2-{k}^{2})}{2+{k}^{2}}}\\{{y}_{2}=\frac{2\sqrt{2}k}{2+{k}^{2}}}\end{array}\right.$,
所以kPQ=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{1}{3}$(k-$\frac{1}{k}$),
因为g(k)=k-$\frac{1}{k}$在(0,$\frac{\sqrt{2}}{2}$)上单调递增,
所以kPQ∈(-∞,-$\frac{\sqrt{2}}{6}$).
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.

| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
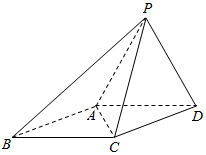 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.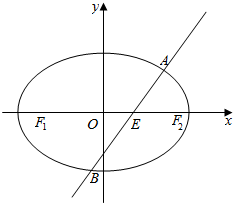 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\sqrt{2}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\sqrt{2}$.