Question

15．已知函数f（x）是定义在R上的奇函数，当x≤0时，f（x）=$\frac{2x}{x-1}$
（1）求f（x）的解析式；
（2）求f（x）在区间[2，6]上的最大值和最小值；
（3）解不等式f[lgx+1g（x-3）]＞f（1）．

Answer 1

分析 （1）通过设x＞0，利用f（x）=-f（-x）及当x≤0时f（x）=$\frac{2x}{x-1}$化简即得结论；
（2）通过（1）可知，当x＞0时f（x）为减函数，进而计算可得结论；
（3）通过（1）可知函数f（x）在R上单调递减，则问题转化为lgx+1g（x-3）＜1，进而只需解不等式0＜x（x-3）＜10，结合定义域计算即得结论．

解答 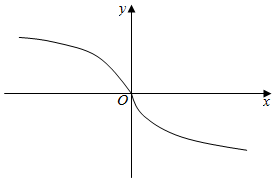解：（1）设x＞0，则-x＜0，
依题意，f（x）=-f（-x）=-$\frac{-2x}{-x-1}$=$\frac{2x}{-x-1}$，
∴f（x）=$\left\{\begin{array}{l}{\frac{2x}{x-1}，}&{x≤0}\\{\frac{2x}{-x-1}，}&{x＞0}\end{array}\right.$；
（2）由（1）可知，f（x）=$\frac{2x}{-x-1}$=-2+$\frac{2}{x+1}$（x＞0），
∴当x＞0时，f（x）为减函数，
∴在区间[2，6]上的最大值和最小值分别为：f（2）=-$\frac{4}{3}$，f（6）=-$\frac{12}{7}$；
（3）由（1）可知，函数f（x）在R上单调递减，
则f[lgx+1g（x-3）]＞f（1）等价于lgx+1g（x-3）＜1，
∴lg[x（x-3）]＜lg10，
又∵函数y=lgx在（0，+∞）上单调递增，
∴0＜x（x-3）＜10，
解得：-2＜x＜0或3＜x＜5，
又∵x＞0，且x-3＞0，
∴3＜x＜5．

点评 本题考查函数的最值及其几何意义，涉及函数的单调性、函数的奇偶性、解不等式等基础知识，注意解题方法的积累，属于中档题．