题目内容
6.(1)已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,2),$\overrightarrow{c}$=(3,4).若λ为实数,($\overrightarrow{a}$+λ$\overrightarrow{b}$)∥$\overrightarrow{c}$,求λ的值.(2)已知非零向量$\overrightarrow{{e}_{1}}$和$\overrightarrow{{e}_{2}}$不共线,欲使向量k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$和$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$共线,试确定实数k的值.
分析 (1)(2)利用向量共线定理即可得出.
解答 解:(1)∵$\overrightarrow{a}$+λ$\overrightarrow{b}$=(1-3λ,2+2λ),∵($\overrightarrow{a}$+λ$\overrightarrow{b}$)∥$\overrightarrow{c}$,∴4(1-3λ)-3(2+2λ)=0,解得$λ=-\frac{1}{9}$.
(2)∵k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$和$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$共线,∴存在实数m,使得k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$=m($\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$),非零向量$\overrightarrow{{e}_{1}}$和$\overrightarrow{{e}_{2}}$不共线,
∴k=m,1=mk,
解得k=1或k=-1.
点评 本题考查了向量共线定理、共面向量基本定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.化简$\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BD}-\overrightarrow{CD}$=( )
| A. | 0 | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
18.直线y=x+a与曲线y=lnx相切时a=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
15.从1、2、3、4、5、6这6个数字中,一次性任取两数,两数都是偶数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
16.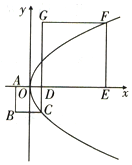 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $1-\frac{{\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $2-\sqrt{2}$ |