题目内容
15．从1、2、3、4、5、6这6个数字中，一次性任取两数，两数都是偶数的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
分析 先求出基本事件总数n=${C}_{6}^{2}$=15，再求出两数都是偶数包含的基本事件个数m=${C}_{3}^{2}$=3，由此能求出两数都是偶数的概率．
解答 解：从1、2、3、4、5、6这6个数字中，一次性任取两数，
基本事件总数n=${C}_{6}^{2}$=15，
两数都是偶数包含的基本事件个数m=${C}_{3}^{2}$=3，
两数都是偶数的概率是p=$\frac{m}{n}=\frac{3}{15}=\frac{1}{3}$．
故选：B．
点评 本题考查概率的求法，考查推理论证能力、运算求解能力，考查转化化归思想，是基础题．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
5．已知A，B分别为椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右顶点，不同两点P，Q在椭圆C上，且关于x轴对称，设直线AP，BQ的斜率分别为m，n，则当$\frac{a}{b}+3\sqrt{mn}$取最小值时，椭圆C的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
3．已知复数z满足（$\sqrt{3}$+3i）z=$\sqrt{3}$i，则z=（ ）
| A． | $\frac{{\sqrt{3}}}{4}+\frac{1}{4}i$ | B． | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | C． | $\frac{{\sqrt{3}}}{4}-\frac{1}{4}i$ | D． | $\frac{1}{4}-\frac{{\sqrt{3}}}{4}i$ |
20．已知数列-3，7，-11，15…，则下列选项能表示数列的一个通项公式的是（ ）
| A． | an=4n-7 | B． | an=（-1）n（4n+1） | C． | an=（-1）n•（4n-1） | D． | an=（-1）n+1•（4n-1） |
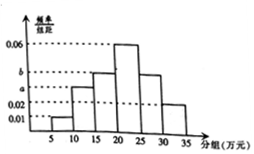某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查，并将结果制作成频率分布直方图，如图，已知样本中数据在区间[10，15）上的人数与数据在区间[25，30）的人数之比为3：4．