题目内容
若函数y=x2+2ax与直线y=2x-4相切,则a= .
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:直线与抛物线相切,联立方程组使方程只有一解,利用判别式进行判定即可.
解答:
解:∵函数y=x2+2ax与直线y=2x-4相切,
∴
,
即x2+(2a-2)x+4=0只有一解
即△=(2a-2)2-4×4=0
解得a=3或a=-1,
故答案为:3或-1.
∴
|
即x2+(2a-2)x+4=0只有一解
即△=(2a-2)2-4×4=0
解得a=3或a=-1,
故答案为:3或-1.
点评:本题主要考查了直线与抛物线相切的解法,以及一元二次方程只有一解的应用,属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
若点(-1,m)在直线x+2y-1=0的上方,则y=
( )
| m2+1 |
| m-1 |
A、有最小值2+2
| ||
B、有最大值2+2
| ||
C、有最大值2-2
| ||
D、有最小值2
|
函数y=sin(3x+
)的图象的一条对称轴是( )
| 3π |
| 4 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|
定义在R上的函数f(x)满足:f′(x)>f(x)恒成立,若x1<x2,则ex1f(x2)与ex2f(x1)的大小关系为( )
| A、ex1f(x2)>ex2f(x1) |
| B、ex1f(x2)<ex2f(x1) |
| C、ex1f(x2)=ex2f(x1) |
| D、ex1f(x2)与ex2f(x1)的大小关系不确定 |
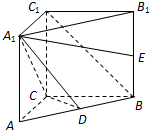 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=