题目内容
已知集合A={0,x,x2-2},则实数x的取值组成的集合是 .
考点:集合的确定性、互异性、无序性
专题:集合
分析:根据集合元素的互异性,可得x≠0,x2-2≠0,x2-2≠x,解得x满足的条件,可得答案.
解答:
解:∵A={0,x,x2-2},
∴x≠0,x2-2≠0,x2-2≠x,
即x≠0,x≠±
,x≠-1,x≠2,
故实数x的取值组成的集合是{x∈R|x≠0,x≠±
,x≠-1,x≠2},
故答案为:{x∈R|x≠0,x≠±
,x≠-1,x≠2}
∴x≠0,x2-2≠0,x2-2≠x,
即x≠0,x≠±
| 2 |
故实数x的取值组成的集合是{x∈R|x≠0,x≠±
| 2 |
故答案为:{x∈R|x≠0,x≠±
| 2 |
点评:本题考查的知识点是集合元素的互异性,根据互异性得到x≠0,x2-2≠0,x2-2≠x是解答的关键.

练习册系列答案
相关题目
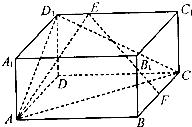 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).