题目内容
若函数f(x)=
x2-2ln(x+1)在其定义域的一个子区间(k,k+
)上不是单调函数,则实数k的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、(
| ||
B、[0,
| ||
C、(
| ||
| D、[0,1) |
考点:利用导数研究函数的单调性
专题:函数的性质及应用
分析:函数f(x)在其定义域的一个子区间(k,k+
)上不是单调函数的意思是:一、区间(k,k+
)是函数定义域的子集,二、区间(k,k+
)的端点应该落在函数f(x)的两个不同的单调区间内.列出满足的不等式组,从而解出k的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:函数的定义域为(-1,+∞),
f′(x)=x-
=
,
当x∈(-1,1)时,f′(x)<0,函数f(x)单调递减,当x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增,
∵函数f(x)在区间(k,k+
)上不是单调函数,∴
解得
<k<1.
故选择:C.
f′(x)=x-
| 2 |
| x+1 |
| (x-1)(x+2) |
| x+1 |
当x∈(-1,1)时,f′(x)<0,函数f(x)单调递减,当x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增,
∵函数f(x)在区间(k,k+
| 1 |
| 2 |
|
| 1 |
| 2 |
故选择:C.
点评:本题考查了函数的单调性,运用了等价转化思想,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
下列说法正确的是( )
①
平行于任何向量;
②若四边形ABCD是平行四边形,则
=
;
③若
•
=0,则
=
或
=
;
④|
•
|=|
|•|
|;
⑤若非零向量
与
满足
∥
,则
与
的夹角为0°.
①
| 0 |
②若四边形ABCD是平行四边形,则
| AB |
| DC |
③若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
④|
| a |
| b |
| a |
| b |
⑤若非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| A、①② | B、②④⑤ |
| C、①⑤ | D、②③⑤ |
已知(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,那么(a0+a2+a4)(a1+a3+a5)的值等于( )
| A、-256 | B、256 |
| C、-512 | D、512 |
已知等差数列{an}中,a3+a7-a10=8,a11-a4=4,记Sn=a1+a2+…+an,则S13=( )
| A、78 | B、152 |
| C、156 | D、168 |
下列几何体中,正视图、侧视图、俯视图都相同的几何体是( )
A、 |
B、 |
C、 |
D、 |
满足条件|z+i|+|z-i|=4的复数z在复平面上对应点的轨迹是( )
| A、一条直线 | B、两条直线 |
| C、圆 | D、椭圆 |
圆(x-2)2+(y+3)2=2的圆心和半径分别是( )
| A、(-2,3),1 | ||
| B、(2,-3),3 | ||
C、(-2,3),
| ||
D、(2,-3),
|
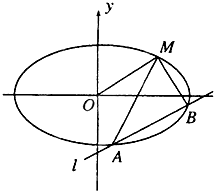 如图,已知椭圆
如图,已知椭圆