题目内容
已知函数f（x）=4cosxsin（x+
）-
（1）求函数f（x）的周期及单调增区间．
（2）函数f（x）的图象可以由函数y=sin2x（x∈R）的图象经过怎样的变换得到？
| π |
| 3 |
| 3 |
（1）求函数f（x）的周期及单调增区间．
（2）函数f（x）的图象可以由函数y=sin2x（x∈R）的图象经过怎样的变换得到？
考点：三角函数中的恒等变换应用,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）先根据两角和与差的正弦公式进行展开后合并，进而再由辅助角公式化简为y=Asin（ωx+φ）的形式，根据T=
可确定周期．
（2））根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
| 2π |
| ω |
（2））根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答：
解：（1）∵f（x）=4cosxsin（x+
）-
=2cosx（
sinx+
cosx）-
=sin2x+
（1+cos2x）-
=sin2x+
cos2x
=2sin（2x+
）
∴函数的最小正周期T=
=π．
由2kπ+
≤2x+
≤2kπ+
，k∈Z，
解得kπ+
≤x≤kπ+
，k∈Z．
所以函数的单调减区间为：[kπ+
，kπ+
]，k∈Z．
（2）由y=sin2x的图象向左平移
个单位可得函数y=sin2（x+
）=sin（2x+
）的图象，
再把所得图象上点的纵坐标变为原来的2倍，可得函数f（x）=2sin（2x+
）的图象．
| π |
| 3 |
| 3 |
=2cosx（
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=sin2x+
| 3 |
| 3 |
=sin2x+
| 3 |
=2sin（2x+
| π |
| 3 |
∴函数的最小正周期T=
| 2π |
| 2 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得kπ+
| π |
| 12 |
| 7π |
| 12 |
所以函数的单调减区间为：[kπ+
| π |
| 12 |
| 7π |
| 12 |
（2）由y=sin2x的图象向左平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
再把所得图象上点的纵坐标变为原来的2倍，可得函数f（x）=2sin（2x+
| π |
| 3 |
点评：本题主要考查两角和与差的正弦定理和辅角公式的应用，考察了函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
从5名学生中选出4名分别参加A，B，C，D四科竞赛，其中甲不能参加A，B两科竞赛，则不同的参赛方案种数为（ ）
| A、24 | B、48 | C、72 | D、120 |
已知函数f（x）=
，若|f（x）|≥kx，则k的取值范围是（ ）
|
| A、（-∞，0] |
| B、（-∞，1] |
| C、[-2，1] |
| D、[-2，0] |
已知椭圆
+
=1（a＞b＞0）的左右焦点分别为F1，F2，点P是椭圆上一点，点M是线段PF1的中点，且|OF1|=2|OM|，OM⊥PF1，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
两人同时向一敌机射击，甲的命中率为
，乙的命中率为
，则两人中恰有一人击中敌机的概率为（ ）
| 1 |
| 5 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
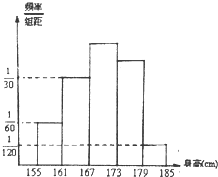某校对高三年级男生的身体发育情况进行调查，共抽取60名男生的身高作为样本，其频率分布直方图如图所示，则身高在[167，179）之间的人数为（ ）一个物体的运动方程为s=1-t+t2其中s的单位是米，t的单位是秒，那么物体在t=4时的瞬时速度是（ ）
| A、7米/秒 | B、6米/秒 |
| C、5米/秒 | D、8米/秒 |