题目内容
奇函数f（x）（x≠0）在（0，+∞）上为增函数，且f（1）=0．那么不等式f（x-1）＜0的解集是 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据函数奇偶性和单调性之间的关系，即可得到结论．
解答：
解：∵奇函数f（x）（x≠0）在（0，+∞）上为增函数，且f（1）=0．
∴在（-∞，0）上为增函数，且f（-1）=-f（1）=0．
则不等式f（x）＜0的解为x＜-1或0＜x＜1，
由x-1＜-1或0＜x-1＜1，
即x＜0或1＜x＜2，
即不等式f（x-1）＜0的解集是{x|x＜0或1＜x＜2}，
故答案为：{x|x＜0或1＜x＜2}
∴在（-∞，0）上为增函数，且f（-1）=-f（1）=0．
则不等式f（x）＜0的解为x＜-1或0＜x＜1，
由x-1＜-1或0＜x-1＜1，
即x＜0或1＜x＜2，
即不等式f（x-1）＜0的解集是{x|x＜0或1＜x＜2}，
故答案为：{x|x＜0或1＜x＜2}
点评：本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设a，b∈R，且a＜b，则（ ）
| A、a2＜b2 | ||||
B、
| ||||
| C、lna＜lnb | ||||
D、a
|
等比数列{an}中，已知，a2=9，公比q为3，则a4=（ ）
| A、27 | B、81 |
| C、243 | D、192 |
已知集合A={x|x＜2}，B={x|x＞a}，且A∩B≠∅，那么a的值可以是（ ）
| A、3 | B、0 | C、4 | D、2 |
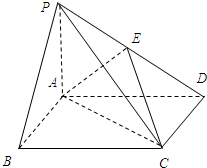如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4，E是PD的中点．