题目内容
命题P:若实数数列{an}是等比数列,满足a24a10a( )=64,则数列{an}的前11项的积为定值.由于印刷问题,括号处的数模糊不清,已知命题P是真命题,则括号处的数为 .
考点:等比数列的性质
专题:等差数列与等比数列
分析:根据等比数列的性质可得:前11项的积为定值即a6为定值,再由等比数列的性质化简a24a10,得到a24a10•a18=a66可得答案.
解答:
解:因为等比数列{an}的前11项的积为定值,则a1a2a3…a11为定值,
由等比数列的性质得,a1a11=a2a10=…=a5a7=a62,
所以a1a2a3…a11=(a62)5•a6=a611为定值,即a6为定值,
因为a24a10=a2a10a23=a62a22•a2,且a2•a18=a102,
所以a24a10•a18=a62(a22a102)=a62(a62)2=a66=64,则a6为定值,
则括号处的数为18,
故答案为:18.
由等比数列的性质得,a1a11=a2a10=…=a5a7=a62,
所以a1a2a3…a11=(a62)5•a6=a611为定值,即a6为定值,
因为a24a10=a2a10a23=a62a22•a2,且a2•a18=a102,
所以a24a10•a18=a62(a22a102)=a62(a62)2=a66=64,则a6为定值,
则括号处的数为18,
故答案为:18.
点评:本题主要考查了等比数列的性质的灵活应用,考查了学生创造性思维和基本的推理能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知集合A={x|x<2},B={x|x>a},且A∩B≠∅,那么a的值可以是( )
| A、3 | B、0 | C、4 | D、2 |
已知平面α、β和直线m,l,则下列命题中正确的是( )
| A、若α⊥β,α∩β=m,l⊥m,则l⊥β |
| B、若α∩β=m,l?α,l⊥m,则l⊥β |
| C、若α⊥β,l?α,则l⊥β |
| D、若α⊥β,α∩β=m,l?α,l⊥m,则l⊥β |
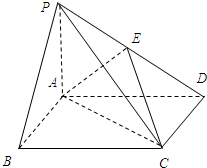 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.