题目内容
已知函数f(x)＝sin2ωx＋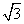
sinωxsin
(ω＞0)的最小正周期为
.
(1) 写出函数f(x)的单调递增区间；
(2) 求函数f(x)在区间
上的取值范围．
解：(1) f(x)＝
＋
sin2ωx＝sin2ωx－
cos2ωx＋＝sin
＋.因为T＝
，所以
＝ (ω＞0)，所以ω＝2，f(x)＝sin
＋.于是由2kπ－≤≤2kπ＋，解得
－
≤x≤＋
(k∈Z)．
所以f(x)的增区间为
(k∈Z)．
(2) 因为x∈，所以4x－∈
，
所以sin∈
，所以f(x)∈
.
故f(x)在区间上的取值范围是.
练习册系列答案
相关题目
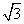asinC－b－c＝0.
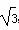，求b、c.
，sinβ＝
，且α、β均为锐角，求α＋β的值．
，则cos2α＋cos2β＋
cosαcosβ＝________．
＝
，则sin(2α＋
)＝__________．
，且α∈
，则sin4α－cos4α＝________．
，则cos(2θ－15°)＝________．
)的周期为π，且图象上有一个最低点为M
.
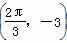的最大值及对应x的值．