题目内容
已知a、b、c分别为△ABC三个内角A、B、C的对边，acosC＋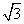
asinC－b－c＝0.
(1) 求A；
(2) 若a＝2，△ABC的面积为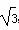
，求b、c.
解：(1) 由acosC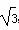＋asinC－b－c＝0及正弦定理得sinAcosC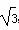＋sinAsinC－sinB－sinC＝0.
因为B＝π－A－C，
所以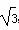sinAsinC－cosAsinC－sinC＝0.
由于sinC≠0，所以sin
＝
.
又0<A<π，故A＝
.
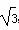(2) △ABC的面积S＝bcsinA＝，故bc＝4.
而a2＝b2＋c2－2bccosA，故b2＋c2＝8.
解得b＝c＝2.
练习册系列答案
名校课堂系列答案
相关题目
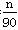(21n－n2－5)(n＝1，2，…，12)，按此预测，在本年度内，需求量超过1.5万件的月份是________．
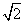，则AC＝________．
＝－
.
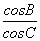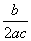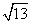，a＋c＝4，求△ABC的面积．
.
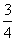的图象，则φ＝________．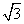
sinωxsin
(ω＞0)的最小正周期为
.
上的取值范围．