题目内容
13.方程|x2-x|+a=0有解,求a的取值范围.分析 方程|x2-x|+a=0有解可化为a=-|x2-x|有解,而由绝对值函数知-|x2-x|∈(-∞,0],从而解得.
解答 解:∵方程|x2-x|+a=0有解,
∴a=-|x2-x|有解,
∵-|x2-x|∈(-∞,0],
∴a∈(-∞,0],
即a的取值范围为(-∞,0].
点评 本题考查了方程与函数的关系应用,同时考查了转化思想与函数思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.设随机变量X~N(2,32),若P(X≤0)=0.1,则P(2≤X<4)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.8 |
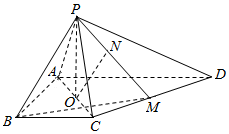 如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.
如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.