Question

下列四个命题：

a

，

b

，

c

为平面向量
（1）若

a

•

b

=

a

•

c

，则

b

=

c

．
（2）若

a

=（1，k），

b

=（-2，6），

a

∥

b

，则k=-3．
（3）非零向量

a

和

b

满足|

a

|=|

b

|=|

a

-

b

|，则

a

与

a

+

b

的夹角为60°．
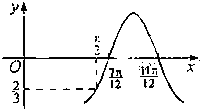
（4）已知函数f（x）=Acos（ωx+φ）的图象如图所示，f（

π

2

）=-

2

3

，则f（0）=

2

3

其中真命题的序号为

 

．（写出所有真命题的序号）

Answer 1

考点：命题的真假判断与应用

专题：简易逻辑

分析：根据向量的数量积的定义，可判断（1），根据向量平行的定义，求出k值，可判断（2），根据向量夹角的定义和几何特征，求出

a

与

a

+

b

的夹角，可判断（3），根据函数f（x）=Acos（ωx+φ）的图象，求出f（0）的值，可判断（4）．

解答： 解：若

a

•

b

=

a

•

c

，则

b

•cos＜

a

，

b

＞=

c

•cos＜

a

，

c

＞，但

b

=

c

不一定成立，故（1）错误；
若

a

=（1，k），

b

=（-2，6），

a

∥

b

，则6+2k=0，解得k=-3，故（2）正确．
非零向量

a

和

b

满足|

a

|=|

b

|=|

a

-

b

|，则

a

与

a

+

b

的夹角为30°，故（3）错误；
由图可得函数f（x）的周期为

2π

3

，则ω=3，f（x）=Acos（3x+φ），由f（

π

2

）=-

2

3

，可得Asinφ=-

2

3

，f（

7π

12

）=0，
可得Acosφ+Asinφ=0，故f（0）=Acosφ=

2

3

，故（4）正确；
故答案为：（2），（4）

点评：本题以命题的真假判断为载体考查了向量的数量积，向量平行与夹角，余弦型函数的图象和性质等知识点，综合性强，难度中档．