题目内容
已知双曲线
-
=1两个焦点为分别为F1,F2,过点F2的直线l与该双曲线的右支交于M,N两点,且△F1MN是以N为直角顶点的等腰直角三角形,则S△F1NM为( )
| x2 |
| 3 |
| y2 |
| b2 |
A、18
| ||
B、12
| ||
| C、18 | ||
| D、12 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设|NF1|=|NM|=m,则|MF1|=
m,再利用双曲线的定义,求出m-2a+
m-2a=m,即4a=
m,由于a2=3,运用三角形的面积公式计算即可得到.
| 2 |
| 2 |
| 2 |
解答:
解:设|NF1|=|MN|=m,
则|MF1|=
m,
由双曲线的定义,
可得|NF2|=m-2a,|MF2|=
m-2a,
∵|NM|=|NF2|+|MF2|=m,
∴m-2a+
m-2a=m,
∴4a=
m,
由于a2=3,
则S△F1NM=
m2=
×8×3=12.
故选D.
则|MF1|=
| 2 |
由双曲线的定义,
可得|NF2|=m-2a,|MF2|=
| 2 |
∵|NM|=|NF2|+|MF2|=m,
∴m-2a+
| 2 |
∴4a=
| 2 |
由于a2=3,
则S△F1NM=
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查双曲线的标准方程与性质,考查双曲线的定义,考查勾股定理和三角形的面积公式,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
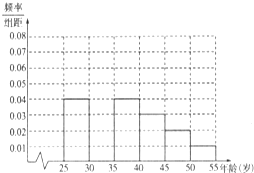 某移动公司对[25,55]岁的人群随机抽取n人进行了一次是否愿意使用4G网络的社会 调查,若愿意使用的称为“4G族”,否则称为“非4G族”,得如下统计表和各年龄段人数频率分布直方图:
某移动公司对[25,55]岁的人群随机抽取n人进行了一次是否愿意使用4G网络的社会 调查,若愿意使用的称为“4G族”,否则称为“非4G族”,得如下统计表和各年龄段人数频率分布直方图: