题目内容
13.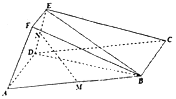 已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点
已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点(Ⅰ)求证:MN∥平面BCEF;
(Ⅱ)求证:平面ADEF⊥平面DEB;
(Ⅲ)若MN=4,求直线MN与平面BDE所成角的正弦值.
分析 (Ⅰ)取EC的中点G,连接GB,GN,推导出四边形MBGN是平行四边形,从而MN∥GB,由此能证明MN∥平面BCEF.
(Ⅱ)推导出AD⊥BD,⊥DE,从而AD⊥平面DEB,由此能证明平面ADEF⊥平面DEB.
(Ⅲ)取BD的中点H,连接MH,NH,则MH∥AD,∠MNH为直线MN与平面BDE所成的角,由此能出直线MN与平面BDE所成角的正弦值.
解答 证明:(Ⅰ)取EC的中点G,连接GB,GN,
∵EN=DN,∴NG∥DC,且NG=$\frac{1}{2}$DC,
又∵AM=BM,四边形ABCD是平行四边形,
∴NG∥MB,且NG=MB,
∴四边形MBGN是平行四边形,∴MN∥GB,
又∵BG?平面BCEF,MN?平面BCEF,
∴MN∥平面BCEF.
(Ⅱ)在△ADB中,∵∠DAB=60°,AB=2AD,∴AD⊥BD,
在梯形ADEF中,∵AD=2EF=2DE=2,AF=$\sqrt{2}$,
∴AD⊥DE,又∵DE∩DB=D,
∴AD⊥平面DEB,
又∵AD?平面ADEF,
∴平面ADEF⊥平面DEB.
解:(Ⅲ)取BD的中点H,连接MH,NH,则MH∥AD,
由(Ⅱ)得AD⊥平面DEB,∴MH⊥平面DEB,
∴NH是MN在平面DEB上的射影,且MH⊥NH,
∴∠MNH为直线MN与平面BDE所成的角,
在Rt△MNH中,MH=$\frac{1}{2}$AD=1,
∴sin$∠MNH=\frac{MH}{MN}=\frac{1}{4}$,
∴直线MN与平面BDE所成角的正弦值为$\frac{1}{4}$.
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
3.设集合A={x|0≤x≤2},B={x∈N|1≤x≤3},则A∩B=( )
| A. | {1,2} | B. | {1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
18.已知a=2ln3,b=2lg2,c=($\frac{1}{4}$)${\;}^{lo{g}_{\frac{1}{3}}\frac{1}{2}}$,则( )
| A. | c>a>b | B. | a>b>c | C. | a>c>b | D. | b>c>a |
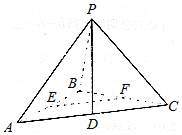 如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.
如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.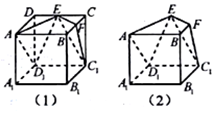 如图,在图(1)的正方体ABCD-A1B1C1D1中,E、F分别为CD、BC的中点,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )
如图,在图(1)的正方体ABCD-A1B1C1D1中,E、F分别为CD、BC的中点,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )