题目内容
8.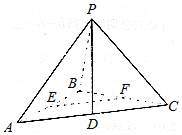 如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.
如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.(1)求证:EF⊥PD;
(2)求直线PF与平面PBD所成的角的正弦值.
分析 (1)连结BD,摔倒导出BD⊥AC,AC⊥PB,从而AC⊥PD,再由EF∥AC,能证明EF⊥PD.
(2)由PB⊥面ABC,得PB⊥EF,连结BD,交EF于点O,则∠FPO为直线PF与平面PBD所成的角,且EF⊥PO,由此能求出直线PF与平面PBD所成的角的正弦值.
解答 证明:(1)连结BD,在△ABC中,∠ABC=90°,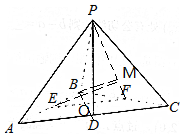
∵AB=BC,点D为AC的中点,∴BD⊥AC,
又PB⊥面ABC,∴AC⊥PB,
又PB与BD交于点B,∴AC⊥平面PBD,AC⊥PD,
∵E,F分别为AB、BC的中点,
∴EF∥AC,∴EF⊥PD.
解:(2)PB⊥面ABC,∴PB⊥EF,
连结BD,交EF于点O,
∵EF⊥PB,EF⊥PD,∴EF⊥平面PBD,
∴∠FPO为直线PF与平面PBD所成的角,且EF⊥PO,
∵PB⊥面ABC,∴PB⊥AB,PB⊥BC,
又∵∠PAB=45°,∴PB=AB=2,
∵OF=$\frac{1}{4}$AC=$\frac{\sqrt{2}}{2}$,
∴PF=$\sqrt{P{B}^{2}+B{F}^{2}}$=$\sqrt{5}$,
在Rt△FPO中,sin$∠FPO=\frac{OF}{PF}$=$\frac{\sqrt{10}}{10}$,
∴直线PF与平面PBD所成的角的正弦值为$\frac{\sqrt{10}}{10}$.
点评 本题考查线线垂直的证明,考查线面角的正弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.已知实数x,y满足条件$\left\{\begin{array}{l}3x+y+3≥0\\ 2x-y+2≤0\\ x+2y-4≤0\end{array}\right.$,则z=x2+y2的取值范围为( )
| A. | [1,13] | B. | [1,4] | C. | $[{\frac{4}{5},13}]$ | D. | $[{\frac{4}{5},4}]$ |
4.已知等差数列{an}的公差d≠0,Sn为其前n项和,若a2,a3,a6成等比数列,且a10=-17,则$\frac{{S}_{n}}{{2}^{n}}$的最小值是( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{8}$ | C. | $-\frac{3}{8}$ | D. | $-\frac{15}{32}$ |
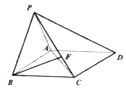 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.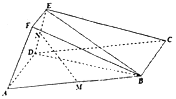 已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点
已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点