题目内容
行列式
的最大值是 .
|
考点:二阶矩阵
专题:选作题,矩阵和变换
分析:
=3
+4
.设
=sinα,则
=cosα,(α∈[0,
],利用辅助角公式,化一角一函数,最后利用正弦函数的有界性即可求出最大值.
|
| x-5 |
| 6-x |
| x-5 |
| 6-x |
| π |
| 2 |
解答:
解:
=3
+4
.
设
=sinα,则
=cosα,(α∈[0,
]
3
+4
=3sinα+4cosα=5sin(α+θ),(tanθ=
)
当α+θ=
时,3
+4
有最大值5
故答案为5
|
| x-5 |
| 6-x |
设
| x-5 |
| 6-x |
| π |
| 2 |
3
| x-5 |
| 6-x |
| 4 |
| 3 |
当α+θ=
| π |
| 2 |
| x-5 |
| 6-x |
故答案为5
点评:本题考查了二阶矩阵,考查换元法在求最值中的应用,做题时应注意观察,找到突破口.

练习册系列答案
相关题目
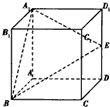 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点. 如图所示,底面直径为10的圆柱被与底面成45°角的平面所截,其截口曲线是一个椭圆,则这个椭圆的离心率为
如图所示,底面直径为10的圆柱被与底面成45°角的平面所截,其截口曲线是一个椭圆,则这个椭圆的离心率为