题目内容
已知数列{an}的前n项和Sn满足Sn=
+
,{bn}为等比数列,且b2=
,b5=-
.
(1)若cn=4+ban,求数列{cn}的通项公式;
(2)设Tn为数列{cn}的前n项和,若对任意的n∈N+,都有p•(Tn-4n)∈[1,3],求实数p的值.
| n2 |
| 2 |
| n |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
(1)若cn=4+ban,求数列{cn}的通项公式;
(2)设Tn为数列{cn}的前n项和,若对任意的n∈N+,都有p•(Tn-4n)∈[1,3],求实数p的值.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)利用递推式可得an,利用等比数列的通项公式可得bn,进而得到cn.
(2)利用等比数列的前n项和公式、数列的单调性即可得出p的取值范围.
(2)利用等比数列的前n项和公式、数列的单调性即可得出p的取值范围.
解答:
解:(1)∵数列{an}的前n项和Sn满足Sn=
+
,
∴当n=1时,a1=S1=
+
=1,
当n≥2时,an=Sn-Sn-1=
+
-[
(n-1)2+
(n-1)]=n.
当n=1时,上式也成立.
∴an=n.
设等比数列{bn}的公比为q,且b2=
,b5=-
.
∴b5=b2q3,∴-
=
×q3,解得q=-
,
∴bn=b2qn-2=
(-
)n-2=(-
)n.
∴cn=4+ban=4+bn=4+(-
)n,即cn=4+(-
)n.
(2)由(1)可得:Tn=4n+
=4n+
[1-(-
)n].
∴p•(Tn-4n)=p
[1-(-
)n].
∵对任意的n∈N+,都有p•(Tn-4n)∈[1,3],
∴1≤p[1-(-
)n]≤3,
∴
≤p≤
,
∴
≤p≤2.
∴实数p的值范围是
≤p≤2.
.
| n2 |
| 2 |
| n |
| 2 |
∴当n=1时,a1=S1=
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=
| n2 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当n=1时,上式也成立.
∴an=n.
设等比数列{bn}的公比为q,且b2=
| 1 |
| 4 |
| 1 |
| 32 |
∴b5=b2q3,∴-
| 1 |
| 32 |
| 1 |
| 4 |
| 1 |
| 2 |
∴bn=b2qn-2=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴cn=4+ban=4+bn=4+(-
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)可得:Tn=4n+
| ||||
1-(-
|
| 1 |
| 3 |
| 1 |
| 2 |
∴p•(Tn-4n)=p
| 1 |
| 3 |
| 1 |
| 2 |
∵对任意的n∈N+,都有p•(Tn-4n)∈[1,3],
∴1≤p[1-(-
| 1 |
| 2 |
∴
| 1 | ||
1-(-
|
| 3 | ||
1-(-
|
∴
| 4 |
| 3 |
∴实数p的值范围是
| 4 |
| 3 |
.
点评:本题考查了递推式的应用、等比数列的通项公式及其前n项和公式、数列的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
下列函数在其定义域内为偶函数的是( )
| A、y=3x | ||
| B、y=sin2x | ||
C、y=
| ||
| D、y=cos2x |
已知直线l:y=x+3与双曲线
-
=1相交于A,B两点,线段AB中点为M,则OM的斜率为( )
| x2 |
| 9 |
| y2 |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
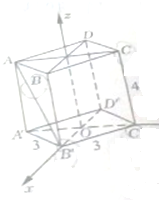 已知长方体ABCD-A′B′C′D′的上,下底面都是边长为3的正方形,长方体的高为4,如图建立空间直角坐标系,求下列直线的一个方向向量.
已知长方体ABCD-A′B′C′D′的上,下底面都是边长为3的正方形,长方体的高为4,如图建立空间直角坐标系,求下列直线的一个方向向量.