题目内容
16.已知关于x的一元二次方程x2+2mx+2m+1=0有两个根,求满足下列条件的m的取值范围.(1)两个根都小于0;
(2)其中一个根在区间(-1,0)内,另一个根在区间(1,2)内.
分析 (1)抛物线f(x)=x2+2mx+2m+1与x轴的两个交点都在区间(-∞,0)中,列出不等式组,求解即可.
(2)抛物线 f(x)=x2+2mx+2m+1与x轴的交点分别在区间(-1,0)和 (1,2)内,列出不等式组求解即可.
解答 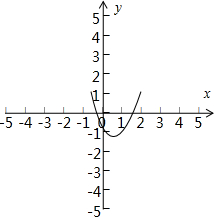 解:(1)由题意知,抛物线f(x)=x2+2mx+2m+1与x轴的两个交点都在区间(-∞,0)中,
解:(1)由题意知,抛物线f(x)=x2+2mx+2m+1与x轴的两个交点都在区间(-∞,0)中,
即$\left\{\begin{array}{l}△=4{m^2}-4({2m+1})≥0\\-m<0\\ f(0)>0\end{array}\right.$解得:$m≥1+\sqrt{2}$.
(2)由题意知,抛物线 f(x)=x2+2mx+2m+1与x轴的交点分别在区间(-1,0)和 (1,2)内,
画出示意图,如图,
得 $\left\{\begin{array}{l}f(0)=2m+1<0\\ f({-1})=2>0\\ f(1)=4m+2<0\\ f(2)=6m+5>0\end{array}\right.⇒\left\{\begin{array}{l}m<-\frac{1}{2}\\ m∈R\\ m<-\frac{1}{2}\\ m>-\frac{5}{6}\end{array}\right.$,
则$-\frac{5}{6}<m<-\frac{1}{2}$.
点评 本题考查二次函数的性质的应用,函数的零点,考查转化思想以及数形结合思想的应用.

练习册系列答案
相关题目
7.已知f(x)=-x+sinx,命题p:?x∈(0,$\frac{π}{2}$),f(x)<0,则( )
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 |
11.已知集合A={-2,-1,0},B={-1,0,1},则A∪B=( )
| A. | {-2} | B. | {-1,0} | C. | {-1,0,1} | D. | {-2,-1,0,1} |
1.给出下列两个命题:
命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$.
命题q:若从一只只有3枚一元硬币和2枚五角硬币的储钱罐内随机取出2枚硬币(假设每枚硬币被抽到都是等可能的),则总共取到2圆钱的概率为$\frac{1}{3}$.那么,下列命题中为真命题的是( )
命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$.
命题q:若从一只只有3枚一元硬币和2枚五角硬币的储钱罐内随机取出2枚硬币(假设每枚硬币被抽到都是等可能的),则总共取到2圆钱的概率为$\frac{1}{3}$.那么,下列命题中为真命题的是( )
| A. | p∧q | B. | ?p | C. | p∧(?q) | D. | (?p)∧(?q) |
8.执行如图的程序框图,则输出的S是( )


| A. | 5040 | B. | 4850 | C. | 2450 | D. | 2550 |